Let x2a2+y2b2=1,a>b, be an ellipse with foci F1 and F2. Let AO be its semi-minor axis. Where O is the centre of the ellipse. The lines AF1 and AF2, when extended, , cut the ellipse again at point B and C respectively. Suppose that the triangle ABC is equilateral. Then the eccentricity of the ellipse is
1√2
1√3
13
12
The correct Answer is:D
mAB=bsinθ−bacosθ=−√3
⇒ba(sinθ−1cosθ)=−√3
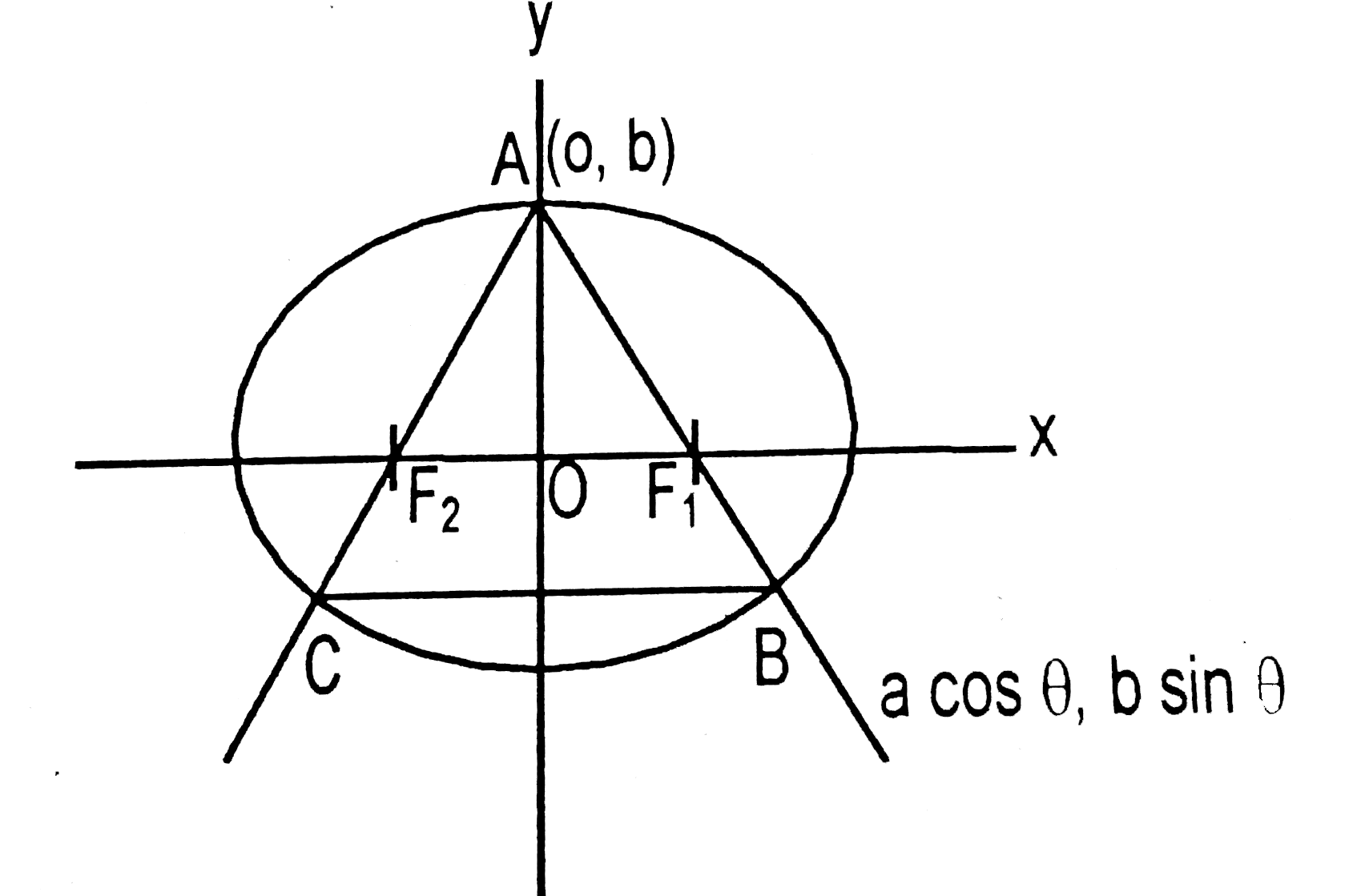
y−b=−√3(x−0)
0+b=+√3ae
b2=3a2e2=a2(1−e2)
⇒4e2=1⇒e=12
Topper's Solved these Questions
- KVPYBOOK - KVPY PREVIOUS YEARCHAPTER - KVPYEXERCISE - PART-2 MATHMATICS
10 Videos
- KVPYBOOK - KVPY PREVIOUS YEARCHAPTER - KVPYEXERCISE - Part 2 Mathematics
15 Videos
- KVPYBOOK - KVPY PREVIOUS YEARCHAPTER - KVPYEXERCISE - Part B- Mathematics
10 Videos
- KVPY 2021BOOK - KVPY PREVIOUS YEARCHAPTER - KVPY 2021EXERCISE - PART II MATHEMATICS
4 Videos
Similar Questions
Chords of the ellipse x2a2+y2b2=1 are drawn through the positive end of the minor axis. Then prove that their midpoints lie on the ellipse.
View SolutionLet x2a2+y2b2=1(b<a). Be an ellipse with major axis AB and minor axis CD. Let F1and F2 be its two foci, with A, F1,F2 B in that order on the segment AB. Suppose ∠F1CB=90∘. The eccentricity of the ellipse is
View Solution
Knowledge Check
S and T are the foci of the ellipse (x2a2)+(y2b2)=1 and B is an end of the minor axis. If STB is equilateral triangle, then eccentricity of the ellipse is
A14B13C12D√32If the angle betweent he lines joining the end points of minor axis of an ellipse with its foci is π2, then the eccentricity of the ellipse is
A12B1√2C√32D12√2If the angle between the lines joining the end points of minor axis of an ellipse with its foci is π2 then the eccentricity of the ellipse is
A1/2B1/√2C√3/√2D1/2√2
If S and S' are two foci of the ellipse x2a2+y2b2=1 and B is and end of the minor axis such that DeltaBSS' is equilateral, then write the eccentricity of the ellipse.
View SolutionLet P be a variable on the ellipse x225+y216=1 with foci at F1andF2
View SolutionIf F1(-3, 4) and F2 (2, 5) are the foci of an ellipse passing through the origin, then the eccentricity of the ellipse is
View SolutionLet S and s' be the foci of an ellipse and B be one end of its minor axis . If SBS' is a isosceles right angled triangle then the eccentricity of the ellipse is
View SolutionLet S and T be the foci of the ellipse x2a2+y2bh2=1 and be an end of the minor axis. If STB is an equilateral triangle, then eccentricity of the ellipse is
View Solution
