Let x2=4ky,k>0 be a parabola with vertex A. Let BC be its latus rectum. An ellipse with center on BC touches the parabola at A, and cuts BC at point D and E such that BD=DE=EC (B,D,E,C in that order). The eccentricity of the ellipse is
1√2
1√3
√53
√32
The correct Answer is:C
n For the parabola,
verter A(0,0)
Four F:(0,k)
end point of latus rectum:
B(-2k,k): c(2k,k)
Length of BC = 4k,
BD=DE=EC
And BD+DE+EC=4k
1⇒BD=DE=EC=4k3…….(i)
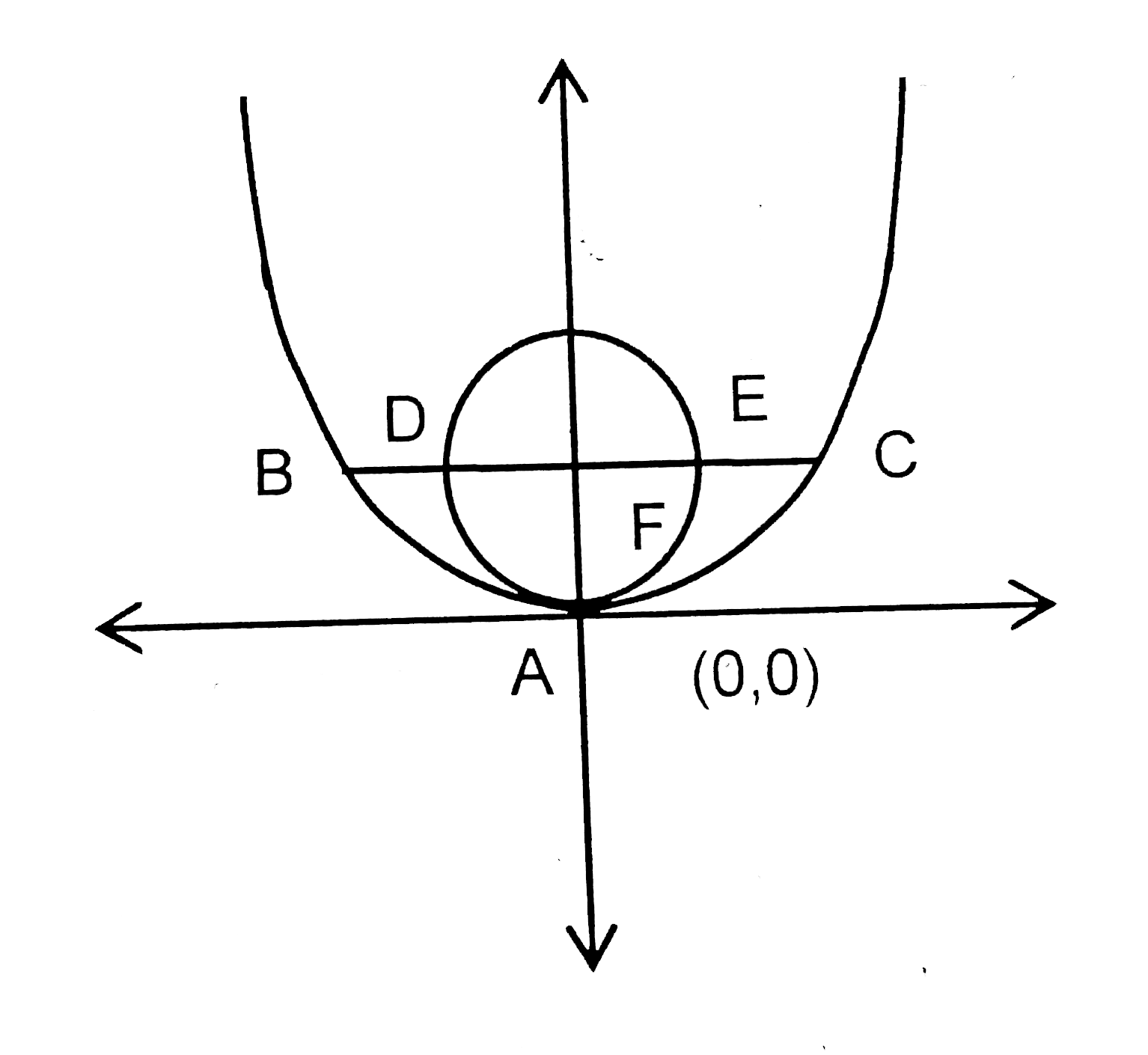
So major Axis of ellipse =2AF= 2× minor Axis of Elllipse =DE=4k3
Eccentricity =C=
⎷1−b2a2=
⎷1−(2k3)2k2 2=√53
Topper's Solved these Questions
- KVPYBOOK - KVPY PREVIOUS YEARCHAPTER - KVPYEXERCISE - PART-2 MATHMATICS
10 Videos
- KVPYBOOK - KVPY PREVIOUS YEARCHAPTER - KVPYEXERCISE - Part 2 Mathematics
15 Videos
- KVPYBOOK - KVPY PREVIOUS YEARCHAPTER - KVPYEXERCISE - Part B- Mathematics
10 Videos
- KVPY 2021BOOK - KVPY PREVIOUS YEARCHAPTER - KVPY 2021EXERCISE - PART II MATHEMATICS
4 Videos
Similar Questions
Knowledge Check
In ΔABC,∠B=90∘. If points D and E are on side BC such that BD=DE=EC, then which is true?
AAE2=5AC2+3AD2B5AE2=2AC2+3AD2C8AE2=3AC2+5AD2D5AE2=3AC2+2AD2ABC is a triangle right- angled at B and D is a point on BC produced (BD>BC), such that BD=2DC. Which one of the following is correct?
AAC2=AD2−3CD2BAC2=AD2−2CD2CAC2=AD2−4CD2DAC2=AD2−5CD2Let a, b and λ positive real numbers. Suppoose P is an end point of the latus rectum of the parabola y2=4λx and suppoose the ellipse x2a2+y2b2=1 passes thorugh the point. P. if the tangents to the parabola and the ellipse at the point P are perpendicular to each other, then the eccentricity of the ellipse is
A1√2B12C13D25
If the ellipse x2a2+y2b2=1(b>a) and the parabola y2=4ax cut at right angles, then eccentricity of the ellipse is
View SolutionIn a triangle ABC, if a=5,b=4andc=3,DandE are the points on BC such that BD=DE=EC. If ΔDAE=θ, then tanθ=
View SolutionIn ΔABC there are 2 points D and E on BC such that BD:DE:EC=3:4:5, if the area of ΔADE=40cm2 then find the area of ΔABC .
View SolutionIn a ABC,D and E are points on sides ABandAC respectively such that BD=CE. If ∠B=∠C, show that DEBC.
View SolutionConsider two straight lines, each of which is tangent to both the circle x2+y2=12 and the parabola y2=4x . Let these lines intersect at the point Q . Consider the ellipse whose center is at the origin O(0, 0) and whose semi-major axis is OQ . If the length of the minor axis of this ellipse is √2 , then which of the following statement(s) is (are) TRUE? For the ellipse, the eccentricity is 1√2 and the length of the latus rectum is 1 (b) For the ellipse, the eccentricity is 12 and the length of the latus rectum is 12 (c) The area of the region bounded by the ellipse between the lines x=1√2 and x=1 is 14√2(π−2) (d) The area of the region bounded by the ellipse between the lines x=1√2 and x=1 is 116(π−2)
View Solution