lf from point perpendiculars to the straight lines and meet at and area of triangle is maximum, then m is equal to
The correct Answer is:4
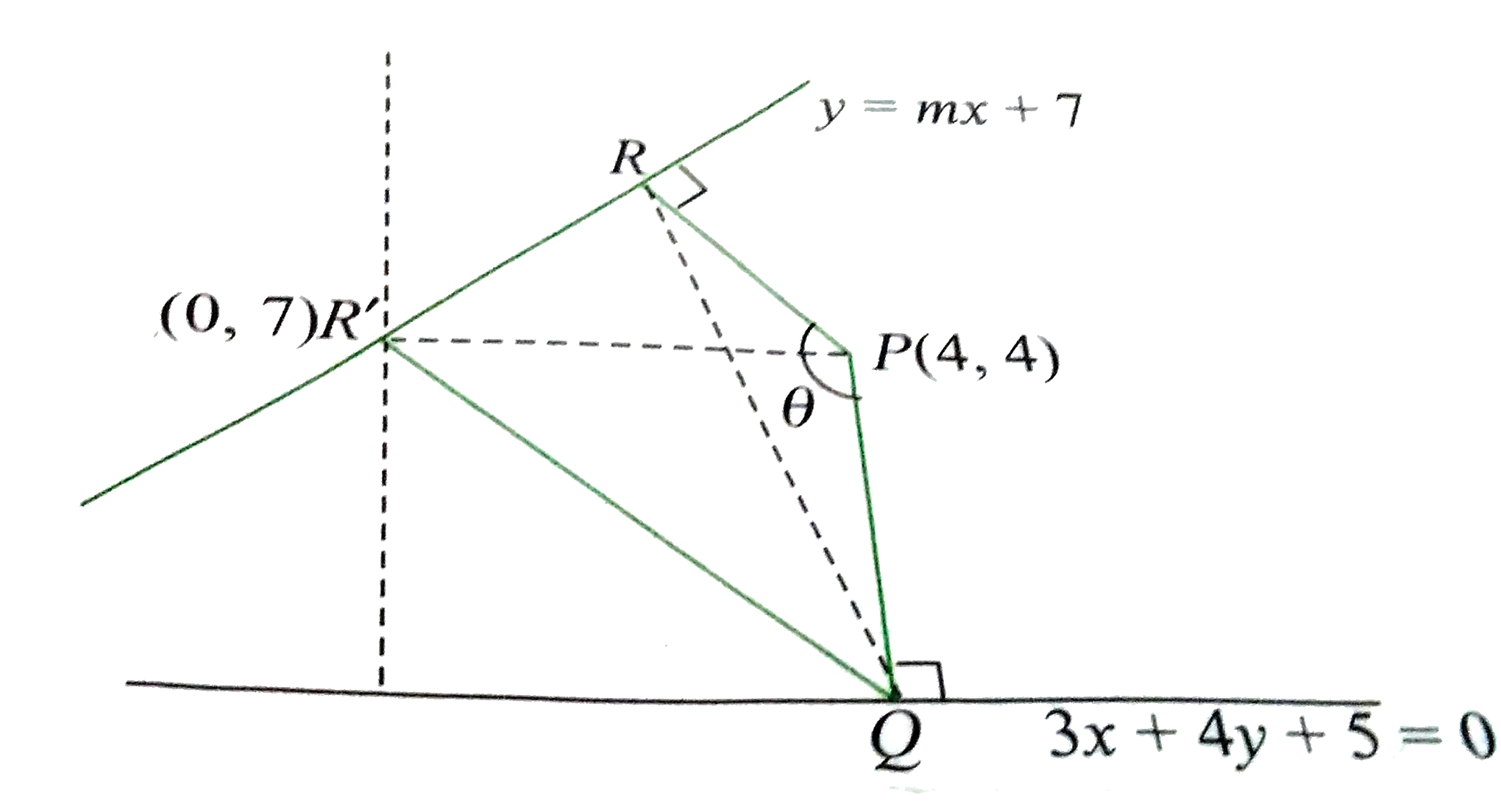
Since PQ is of fixed length,
Area of
This will be maximum if and RP is maximum .
Since passes through it must be rotated about (0,7) such that in new position, becomes i.e., the line becomes perpendicular to , then the slope of line .
That is of = slope of given line. That is the in new position of the line. R coincides with R'.
Topper's Solved these Questions
- COORDINATE SYSYEM BOOK - CENGAGECHAPTER - COORDINATE SYSYEM EXERCISE - JEE Main Previous Year
6 Videos
- COORDINATE SYSYEM BOOK - CENGAGECHAPTER - COORDINATE SYSYEM EXERCISE - Exercise (Matrix)
4 Videos
- COORDINATE SYSTEMBOOK - CENGAGECHAPTER - COORDINATE SYSTEMEXERCISE - Multiple Correct Answers Type
2 Videos
- CROSS PRODUCTS BOOK - CENGAGECHAPTER - CROSS PRODUCTS EXERCISE - DPP 2.2
13 Videos
Similar Questions
lf from point P(4,4) perpendiculars to the straight lines 3x+4y+5=0 and y=mx+7 meet at Q and R area of triangle PQR is maximum, then m is equal to
View SolutionFrom a pointP=(3,4) perpendiculars PQ and PR are drawn to line 3x+4y−7=0 and a variable line y−1=m(x−7) respectively then maximum area of triangle PQR is :
View Solution
Knowledge Check
Area of triangle formed by straight lines 3x+4y=24,x=8andy=1
A12 sq. unitB24 sq. unitC48 sq. unitDNone of theseArea of triangle formed by straight lines 3x−4y=0,x=4 and x-axis
A6 sq. unitB8 sq. unitC12 sq. unitD16 sq. unitThe straight lines x + y - 4 = 0 , 3x + y - 4 = 0 , x + 3y - 4 = 0 form an triangle which is
AisoscelesBright angledCequiateralDscalene
if P,Q are two points on the line 3x+4y+15=0 such that OP=OQ=9 then the area of triangle OPQ is
View SolutionThe straight lines 3x+y−4=0,x+3y−4=0 and x+y=0 form a triangle which is :
View SolutionFrom the point (3 0) 3- normals are drawn to the parabola y2=4x. Feet of these normal are P ,Q ,R then area of triangle PQR is
View SolutionFrom a point P perpendicular tangents PQ and PR are drawn to ellipse x2+4y2=4, then locus of circumcentre of triangle PQR is
View SolutionThe foot of the perpendicular from the point (3, 4) on the line 3x - 4y + 5 = 0 is
View Solution
