Line 4x+5y−7=0 meets the coordinate axes at A and B. Through the mid - point of AB a line is drawn perpendicular to it meeting the line 2x+y=0 at Q(α,β), the value of 1/α−1/β is equal to
The correct Answer is:60
Topper's Solved these Questions
- CARTESIAN SYSTEM OF RECTANGULAR COORDINATES AND STRAIGHT LINES BOOK - MCGROW HILL PUBLICATIONCHAPTER - CARTESIAN SYSTEM OF RECTANGULAR COORDINATES AND STRAIGHT LINES EXERCISE - EXERCISE (CONCEPT - BASED) SINGLE CORRECT ANSWER TYPE QUESTIONS
15 Videos
- CARTESIAN SYSTEM OF RECTANGULAR COORDINATES AND STRAIGHT LINES BOOK - MCGROW HILL PUBLICATIONCHAPTER - CARTESIAN SYSTEM OF RECTANGULAR COORDINATES AND STRAIGHT LINES EXERCISE - EXERCISE (LEVEL 1) SINGLE CORRECT ANSWER TYPE QUESTIONS
60 Videos
- CARTESIAN SYSTEM OF RECTANGULAR COORDINATES AND STRAIGHT LINES BOOK - MCGROW HILL PUBLICATIONCHAPTER - CARTESIAN SYSTEM OF RECTANGULAR COORDINATES AND STRAIGHT LINES EXERCISE - SOLVED EXAMPLES (LEVEL 2) SINGLE CORRECT ANSWER TYPE QUESTIONS
30 Videos
- AREA BY INTEGRATIONBOOK - MCGROW HILL PUBLICATIONCHAPTER - AREA BY INTEGRATIONEXERCISE - Question from Previous Years. B-Architecture Entrance Examination Papers
12 Videos
- CIRCLES AND SYSTEMS OF CIRCLES BOOK - MCGROW HILL PUBLICATIONCHAPTER - CIRCLES AND SYSTEMS OF CIRCLES EXERCISE - QUESTIONS FROM PREVIOUS YEARS. B-ARCHITECTURE ENTRANCE EXAMINATION PAPERS
17 Videos
Similar Questions
Knowledge Check
If the straight line 2x-3y+17-0 is perpendicular to the line passing through the points (7, 17) and (15,β), then β equals
A−5B−353C353D5
Find the equation of the straight line through the point (α,β) and perpendiculasr to the line lx+my+n=0.
View SolutionFind the equation of a line drawn perpendicular to the line x4+y6=1through the point, where it meets the yaxis
View Solutionif the line 4x+3y+1=0 meets the parabola y2=8x then the mid point of the chord is
View SolutionIf the straight line 2x−3y+17=0 is perpendicular to the line passing through the points (7,17) and (15,β), then β equals
View Solutionif the line 4x+3y+1=0 meets the parabola y2=8x then the mid point of the chord is
View SolutionThe line 2x+3y=12 meets the coordinates axes at A and B respectively. The line through (5, 5) perpendicular to AB meets the coordinate axes and the line AB at C, D and E respectively. If O is the origin, then the area (in sq. units) of the figure OCEB is equal to
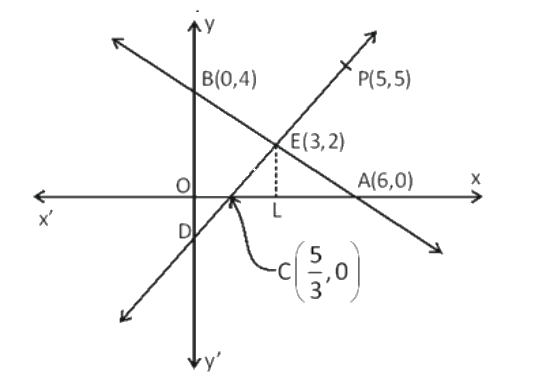
View SolutionThe line 2x+3y=12 meets the coordinates axes at A and B respectively. The line through (5, 5) perpendicular to AB meets the coordinate axes and the line AB at C, D and E respectively. If O is the origin, then the area (in sq. units) of the figure OCEB is equal to

View Solution
