Marks obtaind by 40 students in a short assessment is given below, where a and b are two missing data. If the mean of the distribution is 7.2 find a and b
The correct Answer is:a=1 and b=4
To find the values of a and b given that the mean of the marks obtained by 40 students is 7.2, we can follow these steps:
Step 1: Set Up the Data
We have the following marks and their corresponding frequencies:
- Marks x: 6, 7, 8, 9
- Frequencies f: 6, a, 16, 13, b
Step 2: Calculate xf for Each Mark
We calculate xf (the product of marks and their frequencies):
- For 6: 6×6=36
- For a: 6×a=6a
- For 7: 7×16=112
- For 8: 8×13=104
- For 9: 9×b=9b
The total for xf becomes:
Total xf=36+6a+112+104+9b=252+6a+9b
Step 3: Calculate the Total Frequency
The total frequency ∑f is:
∑f=6+a+16+13+b=35+a+b
Step 4: Set Up the Mean Equation
The mean is given by the formula:
Mean=∑(xf)∑f
Substituting the known values:
7.2=252+6a+9b40
Step 5: Multiply Both Sides by 40
To eliminate the fraction, multiply both sides by 40:
7.2×40=252+6a+9b
Calculating 7.2×40:
288=252+6a+9b
Step 6: Rearranging the Equation
Rearranging gives us:
6a+9b=288−252
6a+9b=36
Step 7: Simplify the Equation
Dividing the entire equation by 3:
2a+3b=12(Equation 1)
Step 8: Set Up the Second Equation
From the total frequency equation:
35+a+b=40
Rearranging gives:
a+b=5(Equation 2)
Step 9: Solve the System of Equations
Now we have two equations:
1. 2a+3b=12
2. a+b=5
From Equation 2, we can express a in terms of b:
a=5−b
Step 10: Substitute into Equation 1
Substituting a into Equation 1:
2(5−b)+3b=12
Expanding gives:
10−2b+3b=12
Combining like terms:
10+b=12
Solving for b:
b=12−10=2
Step 11: Find a
Substituting b=2 back into Equation 2:
a+2=5
Thus,
a=5−2=3
Final Values
The values of a and b are:
a=3,b=2
We have the following marks and their corresponding frequencies:
- Marks x: 6, 7, 8, 9
- Frequencies f: 6, a, 16, 13, b
We calculate xf (the product of marks and their frequencies):
- For 6: 6×6=36
- For a: 6×a=6a
- For 7: 7×16=112
- For 8: 8×13=104
- For 9: 9×b=9b
Total xf=36+6a+112+104+9b=252+6a+9b
The total frequency ∑f is:
∑f=6+a+16+13+b=35+a+b
The mean is given by the formula:
Mean=∑(xf)∑f
Substituting the known values:
7.2=252+6a+9b40
To eliminate the fraction, multiply both sides by 40:
7.2×40=252+6a+9b
Calculating 7.2×40:
288=252+6a+9b
Rearranging gives us:
6a+9b=288−252
6a+9b=36
Dividing the entire equation by 3:
2a+3b=12(Equation 1)
From the total frequency equation:
35+a+b=40
Rearranging gives:
a+b=5(Equation 2)
Now we have two equations:
1. 2a+3b=12
2. a+b=5
a=5−b
Substituting a into Equation 1:
2(5−b)+3b=12
Expanding gives:
10−2b+3b=12
Combining like terms:
10+b=12
Solving for b:
b=12−10=2
Substituting b=2 back into Equation 2:
a+2=5
Thus,
a=5−2=3
The values of a and b are:
a=3,b=2
Topper's Solved these Questions
- MEASURES OF CENTRAL TENDENCY (MEAN, MEDIAN, QUARTILES AND MODE)BOOK - ICSECHAPTER - MEASURES OF CENTRAL TENDENCY (MEAN, MEDIAN, QUARTILES AND MODE)EXERCISE - EXERCISE 24 (D)
8 Videos
- MATRICESBOOK - ICSECHAPTER - MATRICESEXERCISE - Exercise 9D
25 Videos
- MIXED PRACTICE BOOK - ICSECHAPTER - MIXED PRACTICE EXERCISE - SET B
52 Videos
Similar Questions
Marks obtained by 40 students in a short asssessment is given below, where a and b are two missing data.

If the mean of the distribution is 7.2, find a and b.
View SolutionThe marks obtained by 30 students in a class assessment of 5 subjects is given below :

Calculate the mean, median and mode of the above distribution.
View SolutionMarks obtained by 200 students in an examination are given below :
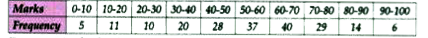
Draw an ogive for the given distribution taking 2 cm = 10 marks on one axis and 2 cm = 20 students on the other axis. Using the graph, determine :
(ii) The number of students who failed if minimum marks required to pass is 40.
View SolutionMarks obtained by 200 students in an examination are given below :

Draw an ogive for the given distribution taking 2 cm = 10 marks on one axis and 2 cm = 20 students on the other axis. Using the graph, determine :
(i) The median marks
View SolutionMarks obtained by 200 students in an examination are given below :

Draw an ogive for the given distribution taking 2 cm = 10 marks on one axis and 2 cm = 20 students on the other axis. Using the graph, determine :
(iii) If scoring 85 and more marks is considered as grade one, find the number of students who secured grade one in the examiantion.
View SolutionThe marks obtained (out of 100) by 400 students in an examination are given below:

Using a graph paper, draw an ogive for the above distribution. Use ogive to estimate:
the number of students who did not pass if the pass percentage was 35.
View SolutionIf the mean of the following distribution is 7.5, find the missing frequency f

View SolutionThe marks obtained by 100 students in a Mathematics test are given below :

Draw an ogive for the given distribution on a graph sheet.
(Use a scale of 2 cm = 10 units on both axis).
Use the ogive to estimate the :
(i) median.
View SolutionThe marks obtained by 100 students in a Mathematics test are given below :

Draw an ogive for the given distribution on a graph sheet.
(Use a scale of 2 cm = 10 units on both axis).
Use the ogive to estimate the :
(ii) lower quartile.
View SolutionThe marks obtained by 100 students in a Mathematics test are given below :

Draw an ogive for the given distribution on a graph sheet.
(Use a scale of 2 cm = 10 units on both axis).
Use the ogive to estimate the number of students who obtained more than 85% marks in the test.
View Solution
