Match the equations A, B, C and D with the lines L1,L2,L3andL4, whose graphs are roughly drawn in the given diagram.
A≡y=2x, B≡y−2x+2=0,
C≡3x+2y=6, D=y=2
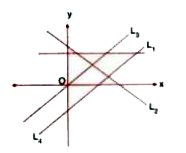
The correct Answer is:A→L3,B→L4,C→L2andD→L1
Step by step video, text & image solution for Match the equations A, B, C and D with the lines L_1, L_2, L_3 and L_4, whose graphs are roughly drawn in the given diagram. A -= y = 2x, " " B -= y - 2x + 2 = 0, C -= 3x + 2y = 6, " "D = y = 2 by Maths experts to help you in doubts & scoring excellent marks in Class 10 exams.
Topper's Solved these Questions
- BOOK - ICSECHAPTER - EQUATION OF A LINEEXERCISE - EXERCISE 14(E)68videos
EQUATION OF A LINE
- BOOK - ICSECHAPTER - EQUATION OF A LINEEXERCISE - EXERCISE 14(C)32videos
EQUATION OF A LINE
- BOOK - ICSECHAPTER - CYLINDER, CONE AND SPHERE EXERCISE - EXERCISE 20 (G)23videos
CYLINDER, CONE AND SPHERE
- BOOK - ICSECHAPTER - FACTORISATIONEXERCISE - M.C.Q(Competency Based Questions )15videos
FACTORISATION
Similar Questions
Match the equations A, B, C, D and E with the lines L1,L2,L3,L4andL5, whose graphs are roughly drawn in the given diagram.
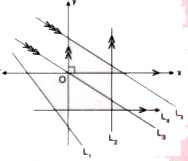
A≡ 2x+y=0, B≡ 2x+y=20
C≡x=8,
D=y=−12 E=2x+3y+12=0View SolutionThe number of triangles that the four lines y=x+3,y=2x+3,y=3x+2, and y+x=3 form is (a) 4 (b) 2 (c) 3 (d) 1
View SolutionThe equation of line l1 is y=2x+3, and the equation of line l2 is y=2x-5.
View SolutionThe equation of a straight line passing through the point (2, 3) and inclined at an angle of tan−1(12) with the line y+2x=5 is: (a)y=3 (b) x=2 (c)3x+4y−18=0 (d) 4x+3y−17=0
View SolutionLet two parallel lines L1 and L2 with positive slope are tangent to the circle C1 : x2+y2−2x16y+64=0. If L1 is also tangent to the circle C2 : x2+y2−2x+2y−2=0 and the equation of L2 is a√ax−by+c−a√a=0 where a,b,c in N. then find the value of a+b+c7
View SolutionThe equation of the circle which touches the axes of coordinates and the line x3+y4+=1 and whose centres lie in the first quadrant is x2+y2−2cx−2cy+c2=0, where c is equal to 4 (b) 2 (c) 3 (d) 6
View SolutionThe equation of the circle which touches the axes of coordinates and the line x3+y4=1 and whose center lies in the first quadrant is x2+y2−2cx−2cy+c2=0 , where c is (a) 1 (b) 2 (c) 3 (d) 6
View SolutionThe equation of the circle which touches the axes of coordinates and the line x3+y4=1 and whose center lies in the first quadrant is x2+y2−2cx−2cy+c2=0 , where c is (a) 1 (b) 2 (c) 3 (d) 6
View SolutionLet L be a normal to the parabola y2=4x. If L passes through the point (9, 6), then L is given by (a) y−x+3=0 (b) y+3x−33=0 (c) y+x−15=0 (d) y−2x+12=0
View SolutionThe number of values of a for which the lines 2x+y−1=0 , ax+3y−3=0, and 3x+2y−2=0 are concurrent is (a).0 (b) 1 (c) 2 (d) infinite
View Solution

