Match the statements/expressions in List I with statements/expressions in List II.

Text Solution
The correct Answer is:a→q,s
We have 2sin2θ+sin22θ=2
⇒2sin2θ+4sin2θcos2θ=2
⇒sin2θ+2sin2θ(1−sin2θ)=1
⇒3sin2θ−2sin4θ−1=0
⇒sinθ=±1√2,±1
⇒θ=π4,π2
Note : Solutions of the remaining parts are given in their respective chapters.
|
Updated on:21/07/2023
Topper's Solved these Questions
- BOOK - CENGAGE ENGLISHCHAPTER - TRIGONOMETRIC EQUATIONSEXERCISE - Exercises (Matrix Match Type)6videos
TRIGONOMETRIC EQUATIONS
- BOOK - CENGAGE ENGLISHCHAPTER - THREE-DIMENSIONAL GEOMETRY EXERCISE - ARCHIVES INTEGER TYPE1videos
THREE-DIMENSIONAL GEOMETRY
- BOOK - CENGAGE ENGLISHCHAPTER - TRIGONOMETRIC FUNCTIONS EXERCISE - SINGLE CORRECT ANSWER TYPE38videos
TRIGONOMETRIC FUNCTIONS
Similar Questions
Knowledge Check
- Question 1 - Select One
Match the statements/expressions given in List I with the values given in List II.
 AabcdsrqpBabcdqsrpCabcdsrpqDabcdqspr
AabcdsrqpBabcdqsrpCabcdsrpqDabcdqspr
Match the conic in List I with the statements/expressions in List II.
 View Solution
View SolutionMatch the statements/expressions given in List ( with the value given in List II.
 View Solution
View SolutionLet f(x)=x2−6x+5x2−5x+6. Then match the expressions/statements in List I with expression /statements in List II.
 View Solution
View SolutionLet f(x)=x2−6x+5x2−5x+6. Then match the expressions/statements in List I with expression /statements in List II.
 View Solution
View SolutionMatch the statements given in the List-I with the equations given in List-II.
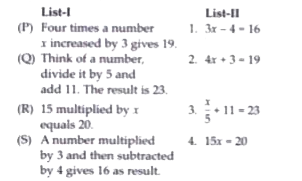 View Solution
View SolutionMatch the statements given in List I with the values given in List II.
 View Solution
View SolutionMatch the statements in List I the appropriate answer in List II.
 View Solution
View Solution




