Number of solutions 2sin(|x|)=4|cosx|∈[−π,π] is equal to
2
4
6
None of these
The correct Answer is:B
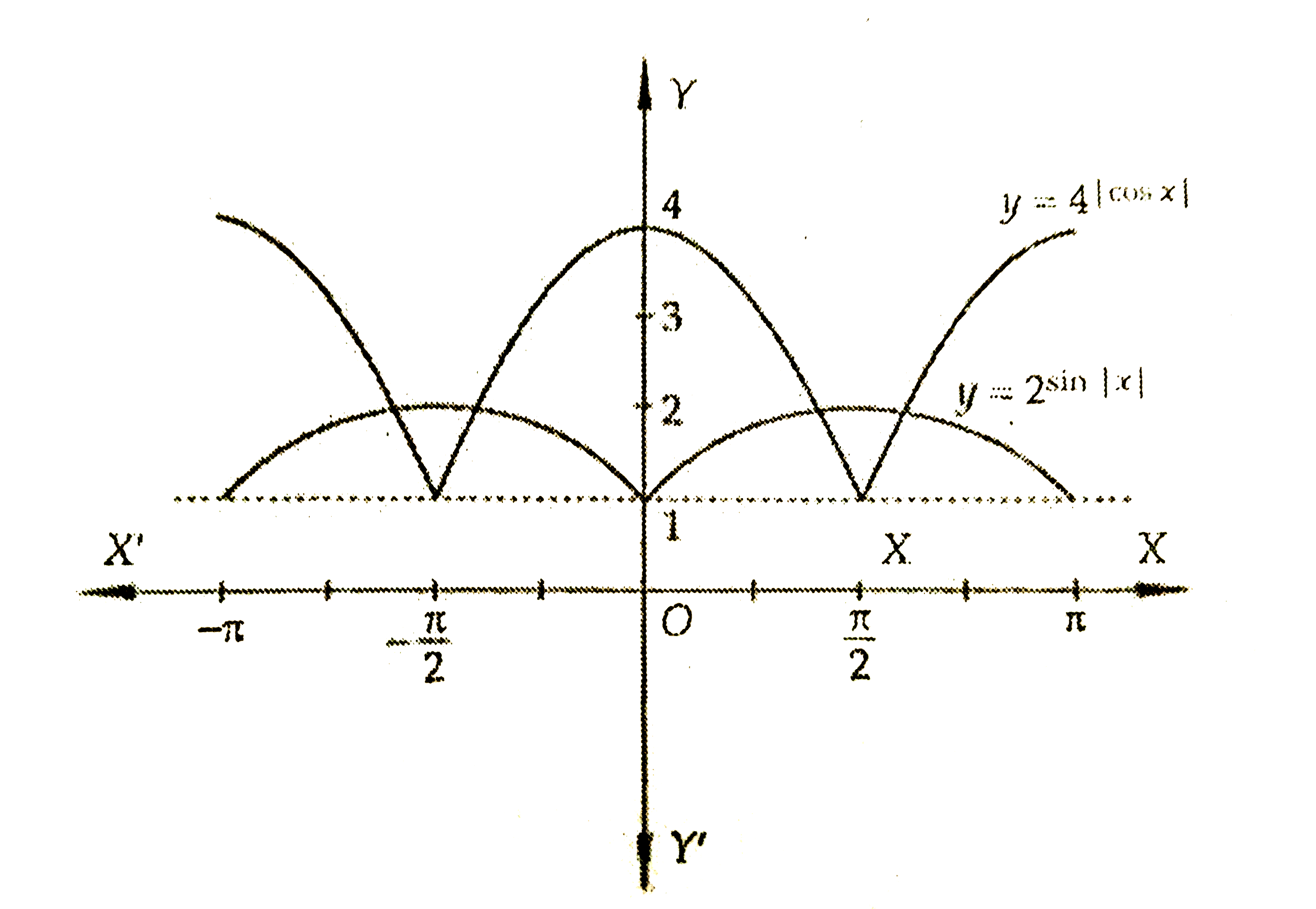
The total number of solutions of the given equation is equal to the number of points of intersection of curves y=4|cosx| and y=2sin|x|. Clearly, these two curves intersect a four points. So, there are four solutions of the given equation in the interval [−π,π].
Topper's Solved these Questions
- MISCELLANEOUS EQUATIONS AND INEQUATIONS Book:OBJECTIVE RD SHARMA ENGLISHChapter:MISCELLANEOUS EQUATIONS AND INEQUATIONS Exercise:Exercise
Explore 30 Videos
- MISCELLANEOUS EQUATIONS AND INEQUATIONS Book:OBJECTIVE RD SHARMA ENGLISHChapter:MISCELLANEOUS EQUATIONS AND INEQUATIONS Exercise:Chapter Test
Explore 29 Videos
- MEASURES OF CENTRAL TENDENCYBook:OBJECTIVE RD SHARMA ENGLISHChapter:MEASURES OF CENTRAL TENDENCYExercise:Chapter Test
Explore 21 Videos
- PLANE AND STRAIGHT LINE IN SPACE Book:OBJECTIVE RD SHARMA ENGLISHChapter:PLANE AND STRAIGHT LINE IN SPACE Exercise:Chapter Test
Explore 31 Videos
Similar Questions
The total number of solutions of loge|sinx|=−x2+2x∈[0,π] is equal to
View SolutionThe total number of solutions of loge|sinx|=−x2+2x∈[0,π] is equal to
View SolutionThe total number of solutions of cosx=√1−sin2x in [0,2π] is equal to
View SolutionThe total number of solution of cosx=√1−sin2x in [0,2π] is equal to (a) 2 (b) 3 (c) 5 (d) none of these
View SolutionThe number of solution of the equation |sinx|=|cos3x| in [−2π,2π] is
View SolutionNumber of solution of sinxcosx−3cosx+4sinx−13>0 in [0,2π] is equal to
View SolutionThe number of solutions of the equation secx1−cosx=11−cosx in [0, 2π] is equal to 3 (b) 2 (c) 1 (d) 0
View SolutionIf f(x)=|cosx|, then f'(π4) is equal to …….
View SolutionNumber of solutions (s) of in |sinx|=−x2 if x∈[−π2,3π2] is/are:
View SolutionThe number of solution of 2cosx=|sinx| where x∈[0.4π] is/are
View Solution