O is the centre of a circle and an equilateral ΔABC is inscribed in it. Find the value of ∠BOC.
The correct Answer is:120∘
To solve the problem of finding the value of angle BOC where O is the center of the circle and ΔABC is an equilateral triangle inscribed in it, we can follow these steps:
1. Understand the Properties of an Equilateral Triangle:
- In an equilateral triangle, all sides are equal and all angles are equal. Therefore, each angle in triangle ABC is 60∘.
2. Identify the Angles:
- Let ∠BAC be one of the angles of the triangle ABC. Since ABC is equilateral, we have:
∠BAC=60∘
3. Use the Circle Theorem:
- According to the theorem of circles, the angle subtended at the center of the circle by an arc is twice the angle subtended at any point on the circumference by the same arc. Therefore, we can express ∠BOC in terms of ∠BAC:
∠BOC=2×∠BAC
4. Substitute the Value of ∠BAC:
- Now substituting the value of ∠BAC:
∠BOC=2×60∘=120∘
5. Final Answer:
- Thus, the value of ∠BOC is:
∠BOC=120∘
- In an equilateral triangle, all sides are equal and all angles are equal. Therefore, each angle in triangle ABC is 60∘.
- Let ∠BAC be one of the angles of the triangle ABC. Since ABC is equilateral, we have:
∠BAC=60∘
- According to the theorem of circles, the angle subtended at the center of the circle by an arc is twice the angle subtended at any point on the circumference by the same arc. Therefore, we can express ∠BOC in terms of ∠BAC:
∠BOC=2×∠BAC
- Now substituting the value of ∠BAC:
∠BOC=2×60∘=120∘
- Thus, the value of ∠BOC is:
∠BOC=120∘
Topper's Solved these Questions
- CIRCLE BOOK - NAGEEN PRAKASHAN ENGLISHCHAPTER - CIRCLE EXERCISE - Exercise 10c
20 Videos
- CIRCLE BOOK - NAGEEN PRAKASHAN ENGLISHCHAPTER - CIRCLE EXERCISE - Revision Exercise (very Short Answer Question)
10 Videos
- CIRCLE BOOK - NAGEEN PRAKASHAN ENGLISHCHAPTER - CIRCLE EXERCISE - Exercise 10a
22 Videos
- AREA OF PARALLELOGRAMS AND TRIANGLESBOOK - NAGEEN PRAKASHAN ENGLISHCHAPTER - AREA OF PARALLELOGRAMS AND TRIANGLESEXERCISE - Revision Exercise (long Answer Question)
5 Videos
- CO-ORDINATE GEOMETRY BOOK - NAGEEN PRAKASHAN ENGLISHCHAPTER - CO-ORDINATE GEOMETRY EXERCISE - Exercise
8 Videos
Similar Questions
In the given figure, an equilateral triangle ABC is inscribed in a circle with centre O. Find :
∠BOC
View SolutionO is the centre of a circle of diameter AB. If chord AC= chord BC, then find the value of ∠ABC.
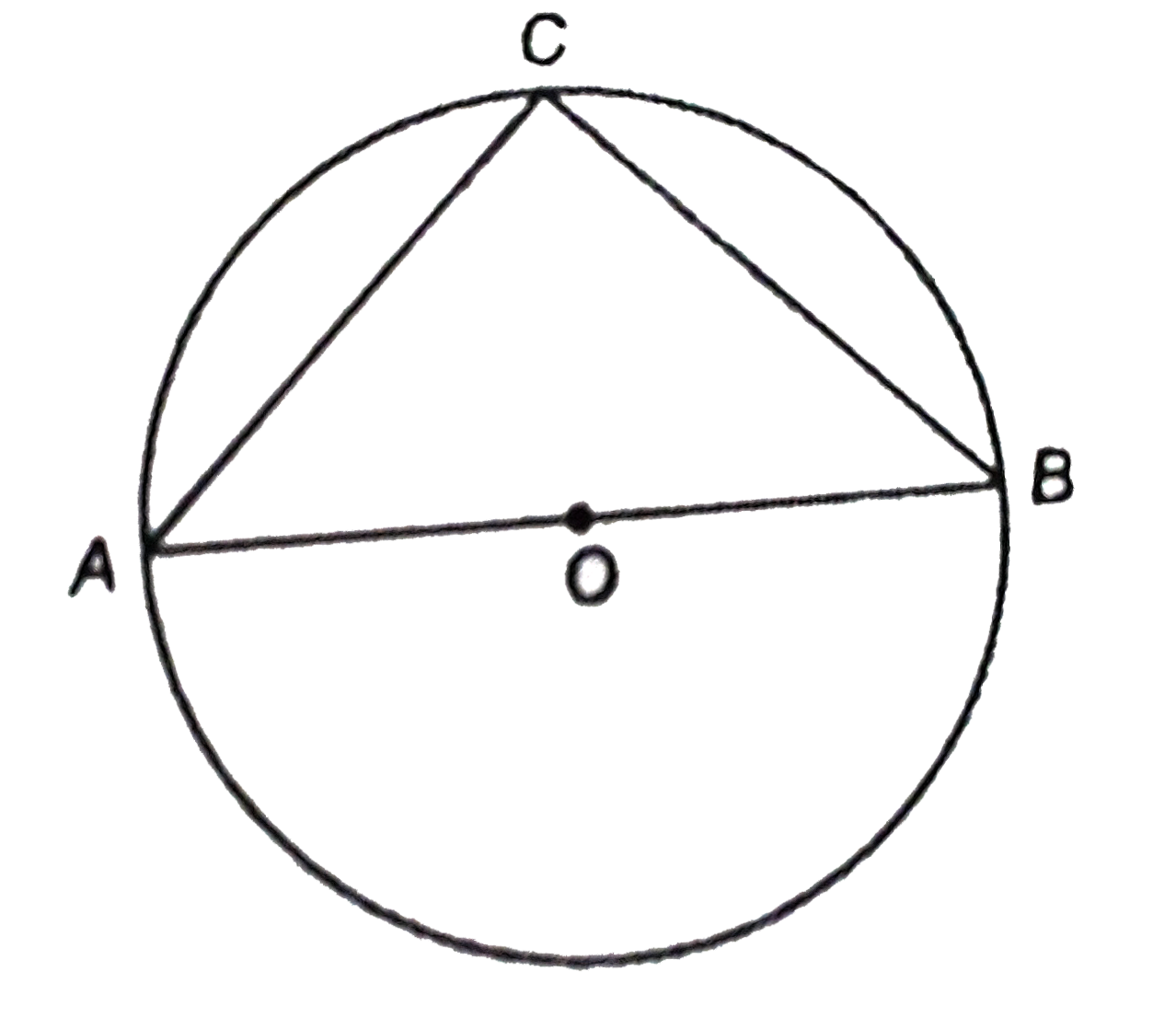
View SolutionIn the given figure, an equilateral triangle ABC is inscribed in a circle with centre O. Find :
∠OBC
View SolutionIn the adjoining figure, O is the centre of the circle. If ∠AOB=150∘ and ∠BOC=100∘, then find the value of ∠ABC.

View SolutionIn the given figure BC//DE and O is the centre of the circle . If ∠CDE=x∘ , find in terms of x∘ the value of ∠BAC.
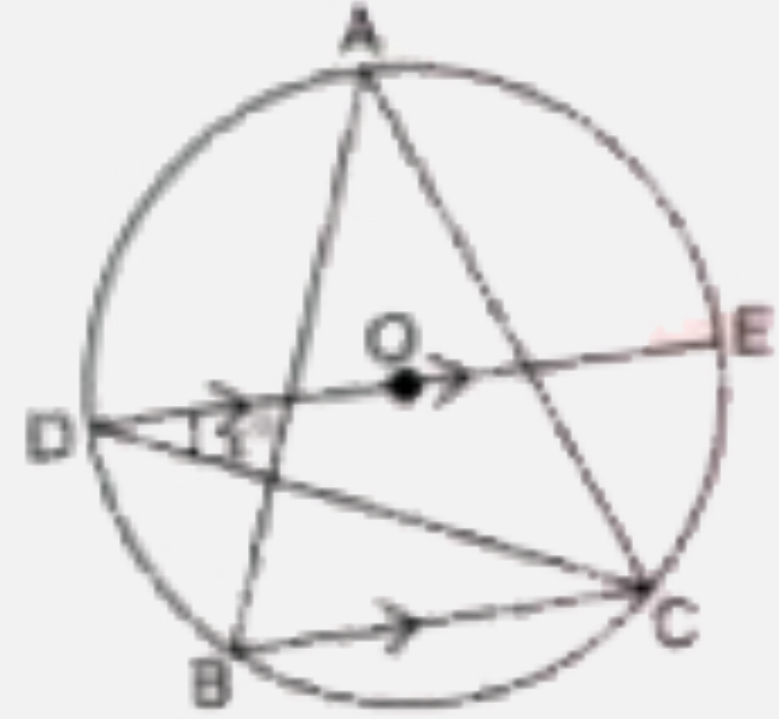
View SolutionIn the adjoining figure, O is the centre of the circle. If ∠PAO=15∘ and ∠PBO=30∘, then find the value of ∠AOB.

View SolutionIn the given on equilateral triangle ABC is inscribed in a ciecle with centre O. Find:
∠OBC and ∠BOC
View SolutionThe circumference of a circle circumscribing an equilateral triangle is 24πunits. Find the area of the circle inscribed in the equilateral triangle.
View SolutionIn the adjoining figure O is the centre of the circle and ∠AOB=100∘. Find the value of ∠BCD.
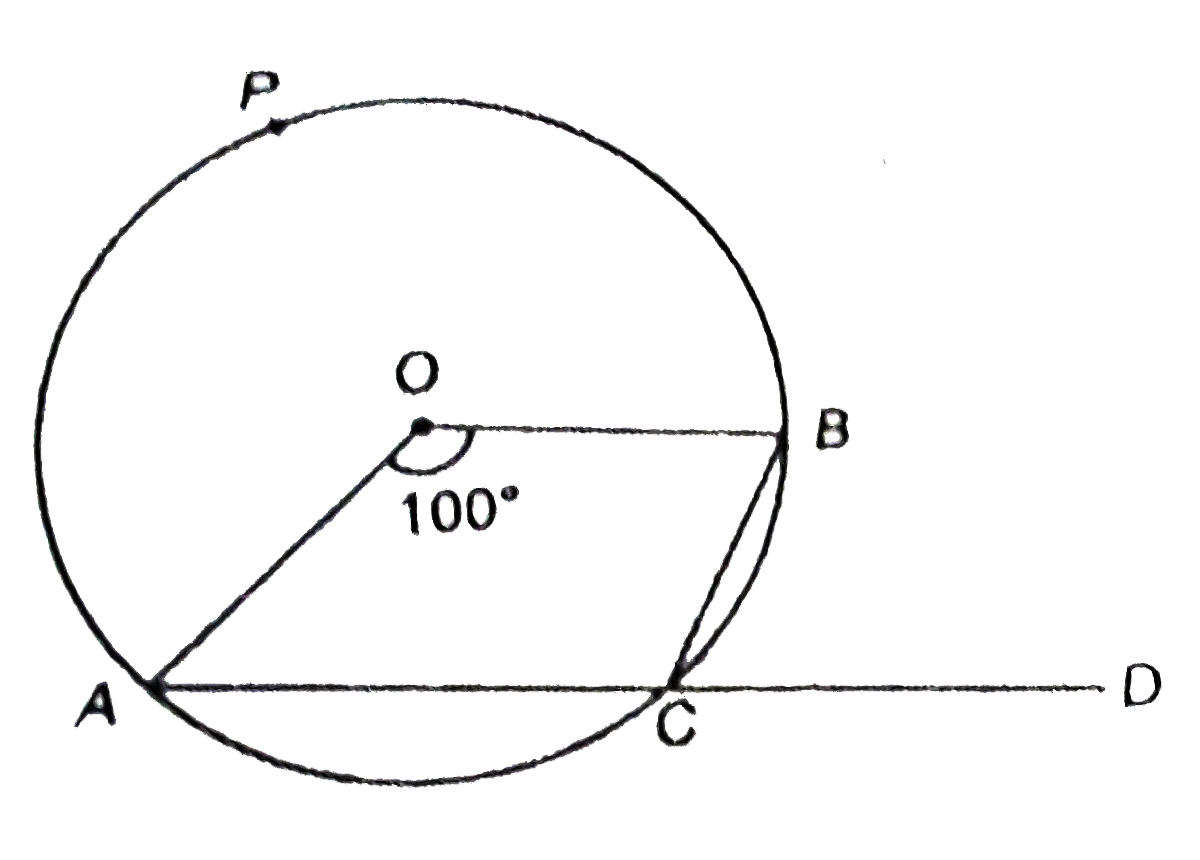
View SolutionIn the adjoining , O is the centre of the circle. ACB is a segment. If ∠OAB=30∘, then find the value of ∠ACB.
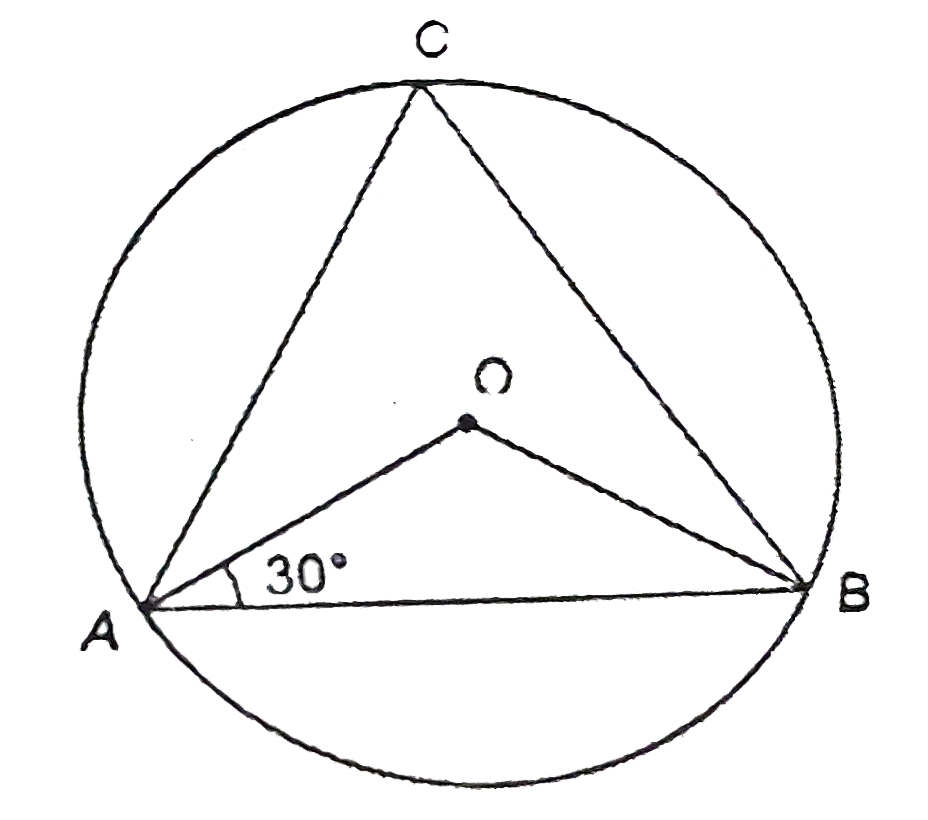
View Solution
