OPQR is a square and M,N are the middle points of the sides PQ and QR, respectively. Then the ratio of the area of the square to that of triangle OMN is
4:1
2:1
8:3
4:3
The correct Answer is:C
Taking the coordinates of the vertics of O,P,Q and R as O(0,0)P (a,0), Q(a,a) and R (0,a) respectively, we get the coordinates of M and N as (a,a/2) and (a/2/a) respectively.
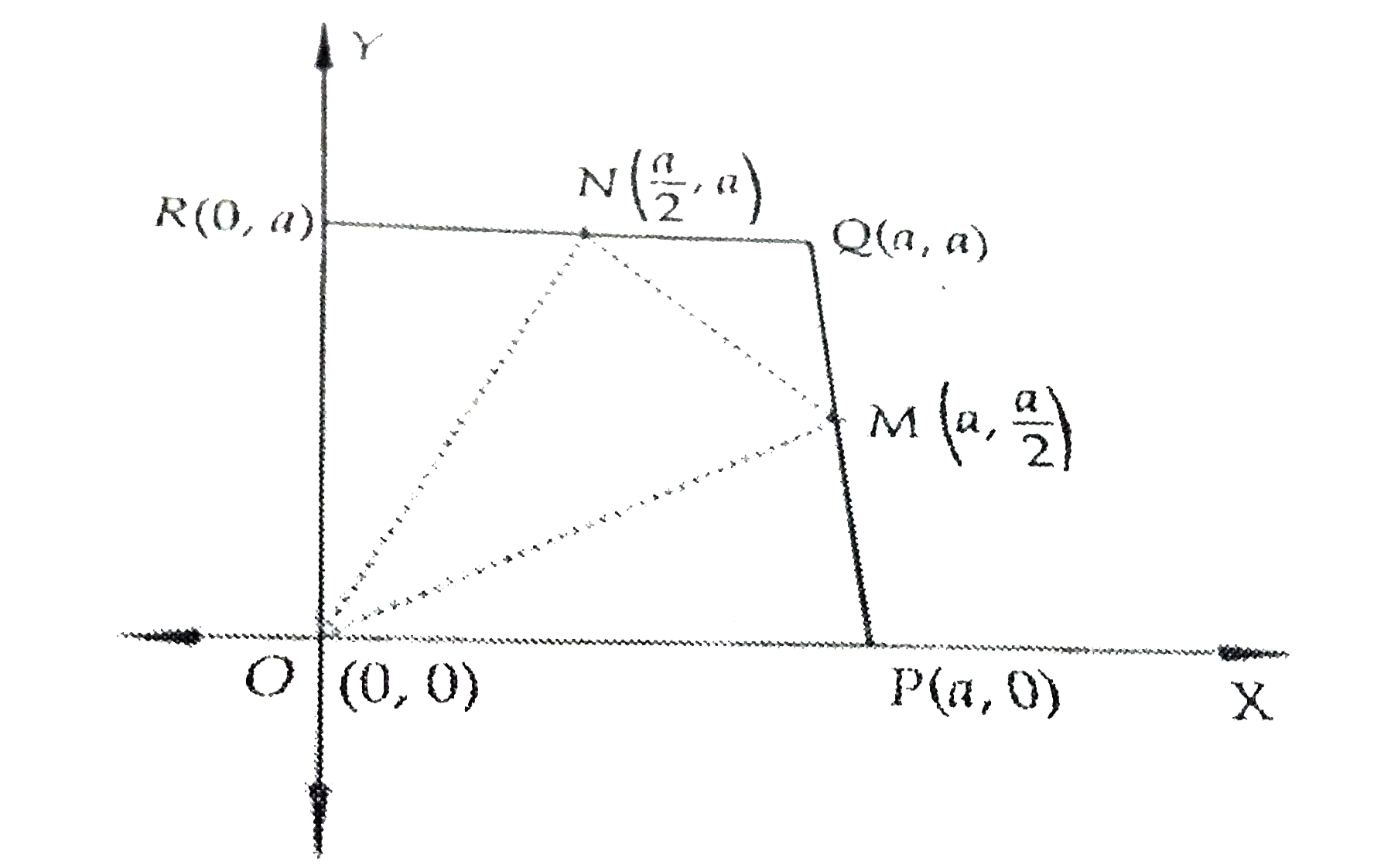
∴Area ofΔOMN=12∣∣
∣
∣∣a01aa/21a/2a1∣∣
∣
∣∣=38a2
∴ Required ratio =8:3
Topper's Solved these Questions
- CARTESIAN CO-ORDINATE SYSTEM BOOK - OBJECTIVE RD SHARMACHAPTER - CARTESIAN CO-ORDINATE SYSTEM EXERCISE - Section II - Assertion Reason Type
6 Videos
- CARTESIAN CO-ORDINATE SYSTEM BOOK - OBJECTIVE RD SHARMACHAPTER - CARTESIAN CO-ORDINATE SYSTEM EXERCISE - Exercise
29 Videos
- CARTESIAN CO-ORDINATE SYSTEM BOOK - OBJECTIVE RD SHARMACHAPTER - CARTESIAN CO-ORDINATE SYSTEM EXERCISE - Exercise
29 Videos
- BINOMIAL THEOREM AND ITS APPLCIATIONS BOOK - OBJECTIVE RD SHARMACHAPTER - BINOMIAL THEOREM AND ITS APPLCIATIONS EXERCISE - Chapter Test
60 Videos
- CONIC SECTIONSBOOK - OBJECTIVE RD SHARMACHAPTER - CONIC SECTIONSEXERCISE - Section I - Solved Mcqs
1 Videos
Similar Questions
OPQR is a square and M,N are the middle points of the sides PQandQR , respectively. Then the ratio of the area of the square to that of triangle OMN is 4:1 (b) 2:1 (c) 8:3 (d) 7:3
View SolutionOPQR is a square and M,N are the midpoints of the sides PQ and QR , respectively. If the ratio of the area of the square to that of triangle OMN is λ:6, then λ4 is equal to 2 (b) 4 (c) 2 (d) 16
View Solution
Knowledge Check
OPQR is a square with M and N as the middle points of the sides PQ and QR, respectively. The ratio of the areas of the square and the triangle OMN is
A4:1B2:1C8:3D4:3OPQR is a square with M and N as the middle points of the sides PQ and QR, respectively. The ratio of the areas of the square and the triangle OMN is
A4:1B2:1C8:3D4:3
In ΔPQR, if PQ=QR and L,M and N are the mid-points of the sides PQ,QR and RP respectively. Prove that LN=MN.

View SolutionConsider a square OABC ,If P and Q are the midpoints of sides AB and BC ,respectively. Then the value of 2(AreaofΔOPQ)Areaof□OABC is
View SolutionABCD is a square of area 1 m2. P and Q are the midpoints of AB and BC respectively. What is the area of Δ DPQ ?
View SolutionLet P, Q, R be the mid-points of sides AB, BC, CA respectively of a triangle ABC. If the area of the triangle ABC is 5 square units, then the area of the triangle PQR is
View SolutionIf PQRS is a square, then write the measure of ∠SRP
View SolutionIf a,b∈N, PQRS is a square and P, Q, R, S are mid points of AB, AD, CD, BC respectively then a+b is
View Solution
