OX and OY are two coordinate axes. On OY a fixed point P(0,c) is taken and on OX any point Q is taken. On PQ, an equilateral triangle is described, its vertex R being on the side of PQ away from O . Then prove that the locus of R is y=√3x−cSolution in Bengali
This given fixed point is P(0,c).
From given fig.,
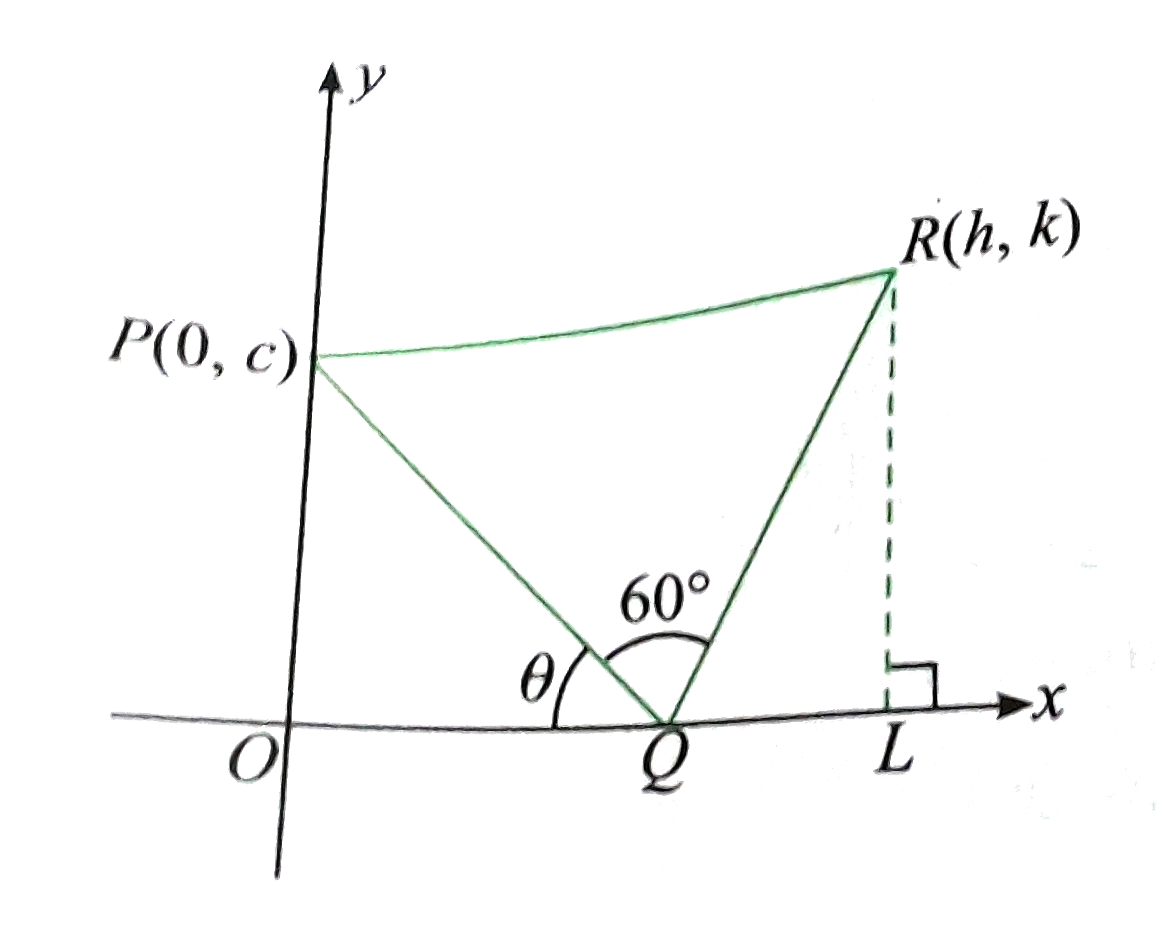
h=OL=OQ+QL
=ccotθ+Qrcos(180∘−60∘−θ)
=ccotθ+PQ{cos120∘.cosθ+sin120∘.sinθ}
=ccotθ−PQ2cosθ+√32PQsinθ
=otθ−12ccosecθcosθ+√32ccosecθsinθ [∵sinθ=cPQ]
∴h=c2(cotθ+√3)(1)
Now, k=RL=RQsin(180∘−60∘−θ)
=PQ{sinθ×12+cosθ×√32}
=ccosecθ{12+sinθ×√32cosθ}
∴ k=c2(1+√3cotθ)
Eliminating cotθ from (1) and (2) , we get k=√3h−c.
Therefore the required locus is y=√3x−c, a straight line.
Topper's Solved these Questions
- COORDINATE SYSYEM BOOK - CENGAGE PUBLICATIONCHAPTER - COORDINATE SYSYEM EXERCISE - Concept applications 1.1
6 Videos
- COORDINATE SYSYEM BOOK - CENGAGE PUBLICATIONCHAPTER - COORDINATE SYSYEM EXERCISE - Concept applications 1.2
8 Videos
- COORDINATE SYSYEM BOOK - CENGAGE PUBLICATIONCHAPTER - COORDINATE SYSYEM EXERCISE - Illustration1.67
1 Videos
- COORDINATE SYSTEMBOOK - CENGAGE PUBLICATIONCHAPTER - COORDINATE SYSTEMEXERCISE - Multiple Correct Answers Type
2 Videos
- CROSS PRODUCTS BOOK - CENGAGE PUBLICATIONCHAPTER - CROSS PRODUCTS EXERCISE - DPP 2.2
13 Videos
Similar Questions
What is the minimum area of a triangle with integral vertices ?
View SolutionFind the distance between the points P(asinα,acosα) and Q(acosα,−asinα)
View SolutionIf A(cosα,sinα),B(sinα,−cosα),C(1,2) are the vertices of ABC, then as α varies, find the locus of its centroid.
View SolutionCoordinates of points on curve 5x2−6xy+5y2−4=0 which are nearest to origin are
View SolutionLet →a and →b be two vectors of equal magnitude 5 units. Let →p,→q be vectors such that →p=→a−→b and →q=→a+→b. If |→p×→q|=2{λ−(→a.→b)2}12, then value of λ is
View SolutionLet O be the origin, and OX,OY,OZ be three unit vectors in the direction of the sides QR , RP , PQ , respectively of a triangle PQR. |OX×OY|= s∈(P+R) (b) sin2R (c)sin(Q+R) (d) sin(P+Q).
View SolutionOX and OY are two coordinate axes. On OY is taken a fixed point P(0,c) and on OX any point Q. On PQ, an equilateral triangle is described, its vertex R being on the side of PQ away from O . Then prove that the locus of R is y=√3x−⋅
View Solutionconsider a point P(4,sqrt(2))o* points Q,R which respectively lie on the lines y=x o* y=0. If Delta PQR is formed and its minimum perimeter is a,then a is equal to
View SolutionOX and OY are two coordinate axes . On OY is taken a fixed point P on OX any point Q . On PQ an equilateral triangle is described, its vertex R being on the side of PQ away from O, then the lacus of R will be,
View SolutionOX and OY are two coordinate axes. On OY a fixed point P(0,c) is taken and on OX any point Q is taken. On PQ, an equilateral triangle is described, its vertex R being on the side of PQ away from O . Then prove that the locus of R is y=√3x−c
View SolutionIf tangents OQ and OR are dawn to variable circles having radius r and the center lying on the rectangular hyperbola xy=1 , then the locus of the circumcenter of triangle OQR is (O being the origin)
(a). xy=4 (b) xy=14 xy=1 (d) none of these
View SolutionABCD is a tetrahedron and O is any point. If the lines joining O to the vertices meet the opposite faces at P,Q,RandS, prove that OPAP+OQBQ+ORCR+OSDS=1.
View SolutionIn Figure, ∠QPR=∠PQR and M and N are respectively on sides QR and PR of PQR such that QM=PN . Prove that OP=OQ, where O is the point of intersection of PM and QN.
View SolutionIf →PO+→OQ=→QO+→OR, show that the point, P,Q,R are collinear.
View SolutionIn Fig. 4.34, A, B and C are points on OP, OQ and OR respectively such that ABPQ and BCQR . Show that ACPR . (FIGURE)
View SolutionLet O be the origin, and OX,OY,OZ be three unit vectors in the direction of the sides QR , RP , PQ , respectively of a triangle PQR. |OX×OY|= (a)sin(P+R) (b) sin2R (c)sin(Q+R) (d) sin(P+Q).
View Solution
