Obtain all zeros of the polynomial (2x3−4x−x2+2), if two of its zeros are √2and(−√2.
The given polynomial is f(x)=2x3−x2−4x+2.
Since √2and−√2 are the zeros of f(x), it follows that each one of (x−√2)and(x+√2) is a factor of f(x).
Consequently , (x−√2)(x+√2)=(x2−2) is a factor of f(x).
On dividing f(x)=2x3−x2−4x+2 by (x2−2), we get
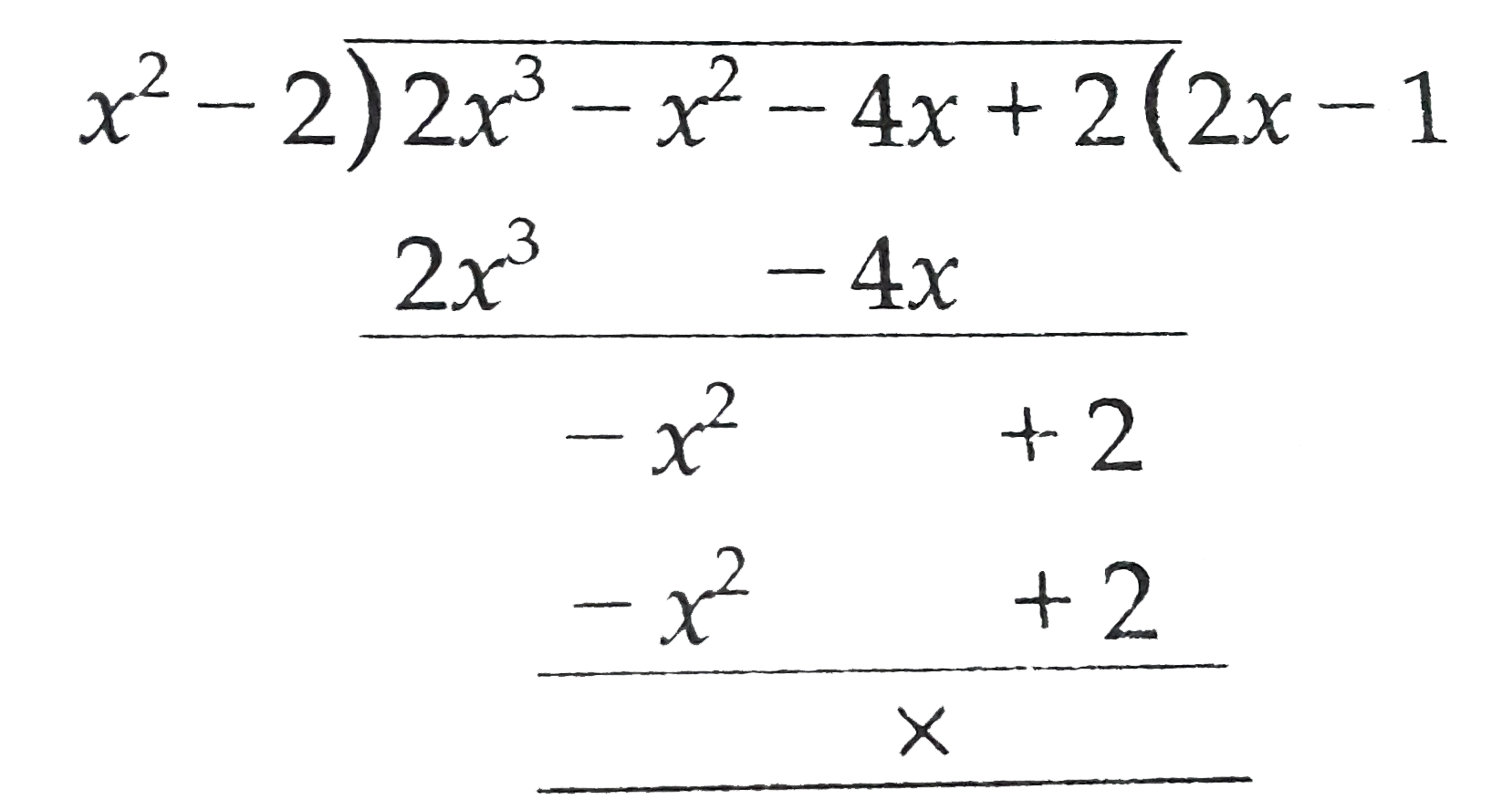
∴f(x)=0⇒(x2−1)(2x−1)=0
⇒(x−√2)(x+√2)(2x−1)=0
⇒(x−√2)=0or(x+√2)=0or(2x−1)=0
⇒x=√2orx=−√2orx=12.
Hence, all zeros of f(x) are √2,−√2and12.
Topper's Solved these Questions
- POLYNOMIALSBOOK - RS AGGARWALCHAPTER - POLYNOMIALSEXERCISE - Exercise 2A
21 Videos
- POLYNOMIALSBOOK - RS AGGARWALCHAPTER - POLYNOMIALSEXERCISE - Exercise 2B
19 Videos
- PERIMETER AND AREA OF PLANE FIGURES BOOK - RS AGGARWALCHAPTER - PERIMETER AND AREA OF PLANE FIGURES EXERCISE - TEST YOURSELF (SHORT -ANSWER QUESTIONS)
1 Videos
- PROBABILITYBOOK - RS AGGARWALCHAPTER - PROBABILITYEXERCISE - Multiple Choice Questions (Mcq)
37 Videos
Similar Questions
Find all the zeroes of the polynomial x3+3x2−2x−6, if two of its zeroes are √2 and −√2.
View SolutionFind all zeros of the polynomial f(x)=x3+3x2−2x−6 , if two of its zeros are −√2 and √2 .
View SolutionObtain all zeros of the polynomial f(x)=x4−3x3−x2+9x−6 , if two of its zeros are −√3 and √3 .
View SolutionFind all zeros of the polynomial 2x4+7x3−19x2−14x+30, if two of its zeros are √2and−√2 .
View SolutionFind all zeros of the polynomial f(x)=2x3+x2−6x−3 , if two of its zeros are −√3 and √3 .
View SolutionFind all the zeros of the polynomial x4+x3−34x2−4x+120, if two of its zeroes are 2 and -2
View SolutionObtain all zeros of the polynomial f(x)=2x4+x3−14x2−19x−6 , if two of its zeros are −2 and 1 .
View SolutionFind all zeros of the polynomial f(x)=x4+x3−34x2−4x+120 , if two of its zeros are 2 and −2 .
View SolutionFind all the zeroes of the polynomial 2x3+x2−6x−3, if two of its zeroes are −√3and√3.
View SolutionObtain the zeroes of the polynomial 4x4+x3−72x2−18x if two of its zeroes are 3√2 and −3√2
View Solution
