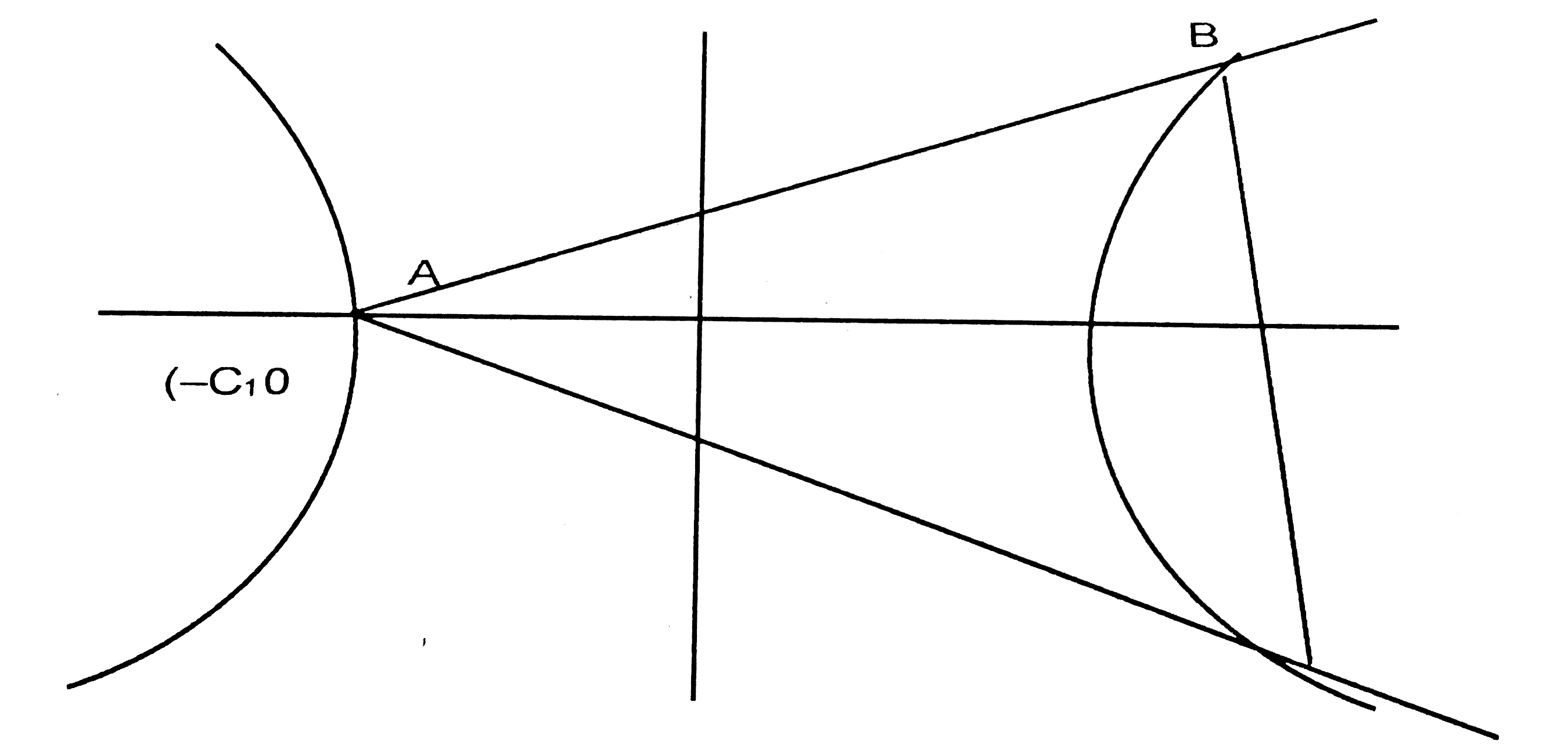
On a rectangular hyperbola $x^{2} - y^{2} = a^{2}, a > 0$ , three points A,B,C are taken as follows : A = (-a,0): B and C are placed symmetrically with respect to the x-axis on the branch of the hyperbola not containing A suppose that the triangle ABC is equilateral. If the side-length of the triangle ABC is ka,then k lies in the interval

(0,2]

(2,4]

(4,6]

(6,8]

Video Solution

Text Solution

Verified by Experts

The correct Answer is:B

Updated on:21/07/2023

Let D be the middle point of the side BC of a triangle ABC. If the triangle ADC is equilateral, then $a^{2} : b^{2} : c^{2}$ is equal to
A $1 : 4 : 3$
B $4 : 1 : 3$
C $4 : 3 : 1$
D $3 : 4 : 1$
If sides of triangle ABC are a, b, and c such that $2 b = a + c$ , then
A $\frac{b}{c} > \frac{2}{3}$
B $\frac{b}{c} > \frac{1}{3}$
C $\frac{b}{c} < 2$
D $\frac{b}{c} < \frac{3}{2}$
If $α, β, γ$ are the parameters of points A,B,C on the circle $x^{2} + y^{2} = a^{2}$ and if the triangle ABC is equilateral ,then
A $\sum cos α = 0$
B $\sum sin α = 0$
C $\sum tan α = 0$
D $\sum cot α = 0$