On the same side of a tower, two objects are located. When observed from the top of the tower, their angles of depression are 45o and 60o . If the height of the tower is 150m, find the distance between the objects.
To solve the problem step-by-step, we will analyze the situation using trigonometric principles.
1. Understand the Problem: We have a tower of height 150 m. From the top of the tower, two objects are observed at angles of depression of 45° and 60°.
2. Draw the Diagram:
- Let A be the top of the tower and B be the base of the tower.
- Let C be the position of the object observed at an angle of depression of 60°, and D be the position of the object observed at an angle of depression of 45°.
3. Identify the Right Triangles:
- Triangle ABC (where angle ACB = 60°)
- Triangle ABD (where angle ADB = 45°)
4. Calculate the Distance from the Tower to Object C:
- In triangle ABC, we can use the tangent function:
tan(60∘)=Height of the towerDistance from tower to object C (BC)
tan(60∘)=√3(since tan(60∘)=√3)
√3=150BC
Rearranging gives:
BC=150√3≈86.6 m
5. Calculate the Distance from the Tower to Object D:
- In triangle ABD, we use the tangent function again:
tan(45∘)=Height of the towerDistance from tower to object D (BD)
tan(45∘)=1(since tan(45∘)=1)
1=150BD
Rearranging gives:
BD=150 m
6. Calculate the Distance Between the Two Objects (CD):
- The distance between the two objects is given by:
CD=BD−BC
Substituting the values we found:
CD=150−86.6=63.4 m
Final Answer:
The distance between the two objects is approximately 63.4 meters.
- Let A be the top of the tower and B be the base of the tower.
- Let C be the position of the object observed at an angle of depression of 60°, and D be the position of the object observed at an angle of depression of 45°.
- Triangle ABC (where angle ACB = 60°)
- Triangle ABD (where angle ADB = 45°)
- In triangle ABC, we can use the tangent function:
tan(60∘)=Height of the towerDistance from tower to object C (BC)
tan(60∘)=√3(since tan(60∘)=√3)
√3=150BC
Rearranging gives:
BC=150√3≈86.6 m
- In triangle ABD, we use the tangent function again:
tan(45∘)=Height of the towerDistance from tower to object D (BD)
tan(45∘)=1(since tan(45∘)=1)
1=150BD
Rearranging gives:
BD=150 m
- The distance between the two objects is given by:
CD=BD−BC
Substituting the values we found:
CD=150−86.6=63.4 m
The distance between the two objects is approximately 63.4 meters.
Topper's Solved these Questions
Similar Questions
Two people standing on the same side of a tower in a straight line with it, measure the angles of elevation of the top of the tower as 25∘and50∘ respectively. If the height of the tower is 70 m, find the distance between the two people
View SolutionTwo man are on the opposite sides of a tower. They measure the angles of elevation the top of the tower as 30∘ and 60∘. If the height of the tower is 150 m, find the distance between the two men.
View SolutionTwo points A and B are on the same side of a tower and in the same straight line with its base. The angles of depression of these points from the top of the tower are 60∘ and 45∘ respectively. If the height of the tower is 15 m, then find the distance between these points.
View SolutionTwo men are on the opposite sides of a tower. They measure the angles of elevation of the top of the tower as 45∘ and 30∘ respectively. If the height of the tower is 40 m, then the distance between the men is
View SolutionAt one side of a road, there os a house and on the other side there is a tower. House and tower are on the same horizontal plane. The angle of depression of the top and foot of the house, from the top of the tower are 30∘ and 45∘ respectively. If the height of the house is 10 m, then find the distance between the house and the tower.
View SolutionIn figure, the angle of elevation of the top of a tower AC from a point B on the ground is 60∘. If the height of the tower is 20m , find the distance of the point from the foot of the tower.
View SolutionIn figure, the angle of elevation of the top of a tower AC from a point B on the ground is 60∘. If the height of the tower is 20m , find the distance of the point from the foot of the tower.
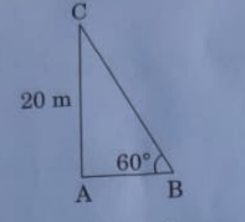 View Solution
View SolutionThe distance between two towers is 140 m while seeing from the top if the second tower, the angle of elevation of first tower is 30∘.If the height of the second tower is 60 m, then find the height of the first tower.
View SolutionThe angle of depression of a car parked on the road from the top of the 150 m high tower is 30∘.Find the distance of the car from the tower
View SolutionThe angular depression of the top and the foot of the chimney seen from the top of a tower on the same base level as the chimney are tan−1(43) and tan−1(52) respectively if the height of the tower is 150m. then the distance between the top of the chimney and the tower is
View Solution

