On the xy plane where O is the origin, given points, A(1,0),B(0,1)andC(1,1). Let P,Q,andR be moving points on the line OA,OB,OC respectively such that ¯¯¯¯¯¯OP=45t¯¯¯¯¯¯¯¯¯(OA),¯¯¯¯¯¯OQ=60t¯¯¯¯¯¯¯¯¯(OB),¯¯¯¯¯¯OR=(1−t)¯¯¯¯¯¯¯¯¯(OC) with t>0. If the three points P,QandR are collinear then the value of t is equal to
A 1106
B 7187
C 1100
D none of these
1106
7187
1100
none of these
The correct Answer is:B
Again it is given that the point P,Q and R are collinear
⇒−−→PQ=λ−−→QR
⇒15r(4→j−3→i)=λ[(1−t)(ˆi+ˆj)−60tˆj]
=λ[(1−t)ˆi+(1−6<ˆj)]
⇒45tt−1=4t1−61t
⇒3(1−61t)=4(t−1)
⇒3−183t=4t−4
⇒187t=7
⇒t=7187
Topper's Solved these Questions
Similar Questions
Knowledge Check
The endpoints of ¯¯¯¯¯¯AB are A(0, 0) and B(9, -6). What is an equation of the line that contains the reflection of ¯¯¯¯¯¯AB in the y-axis?
Ay=−32xBy=−23xCy=−x+3Dy=23x

In the figure above, ¯¯¯¯¯¯AB,¯¯¯¯¯¯CD,and¯¯¯¯¯¯EF all intersect. What is the value of n?
View SolutionLet A and B be two events such that P¯¯¯¯¯¯¯¯¯¯¯¯¯(A∪B)=16,P(A∩B)=14andP¯¯¯A=14,where ¯¯¯A stands for complement of event A. then , events A and B are
View SolutionLet A and B be two events such that P¯¯¯¯¯¯¯¯¯¯¯¯¯(A∪B)=16,P(A∩B)=14andP¯¯¯A=14,where ¯¯¯A stands for complement of event A. then , events A and B are
View Solution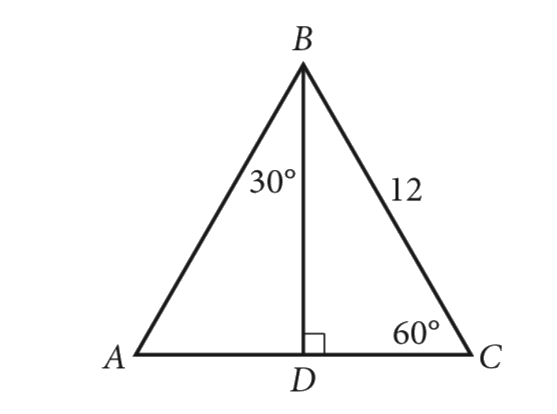
In ΔABC what is the length of ¯¯¯A?
View Solution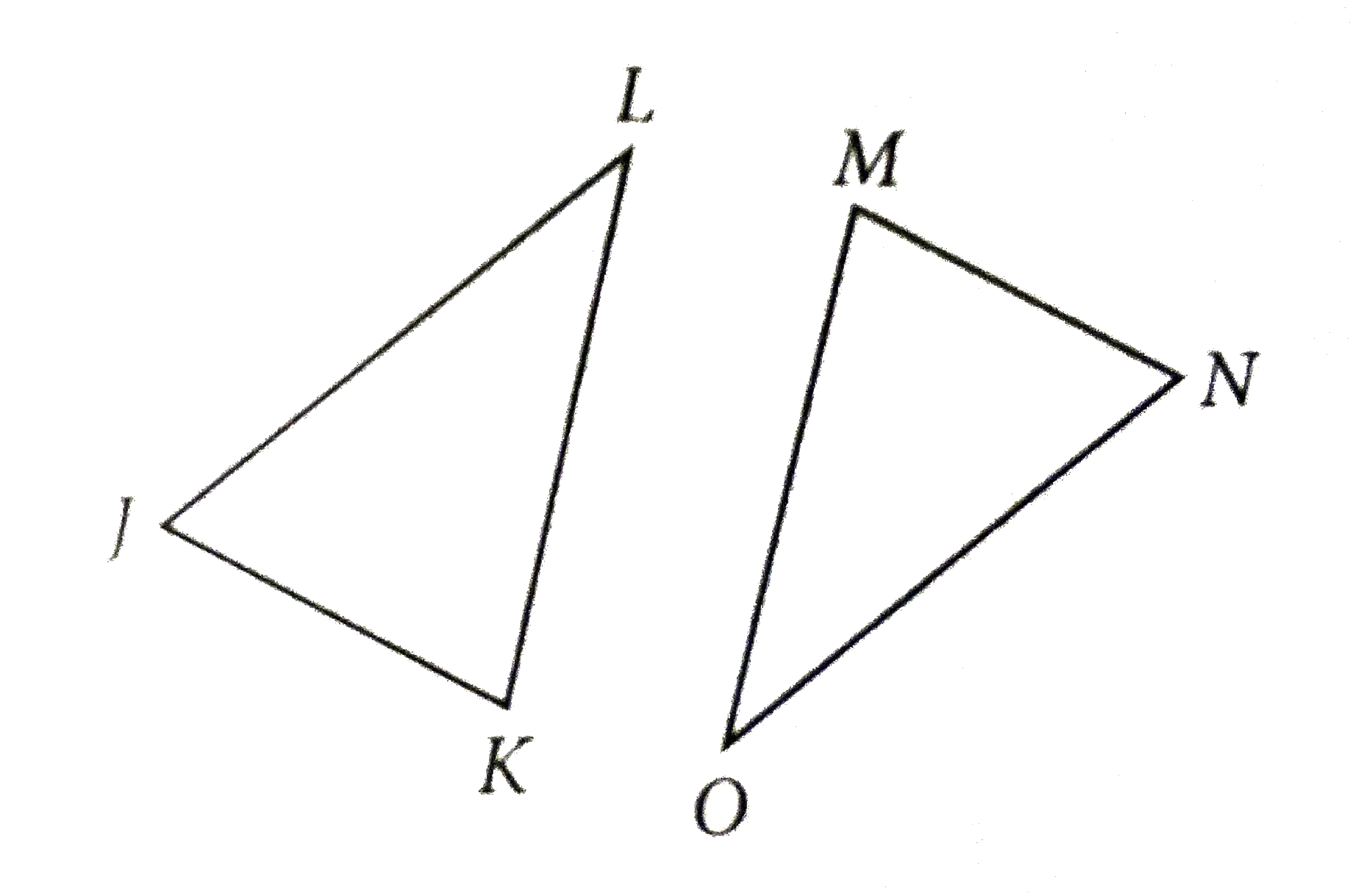
In the diagram above, ¯¯¯¯¯JL=¯¯¯¯¯¯ONand¯¯¯¯¯¯KL=¯¯¯¯¯¯¯OM. Confirmation of which of the following facts would be sufficient to prove that the two triangles are congruent?
View SolutionIf P(A∩B)=12,P(¯¯¯A∩¯¯¯B)=12 and 2P(A)=P(B)=p, then the value of p is equal to
View Solution¯xand¯y be two variable vectors satisfying simultaneous vector equation
¯x+¯cׯy=¯a
¯y+¯cׯx=¯b where ¯c is a non zero vector . Then the value of ¯xand¯y is given by
View Solution
