If the points (0,0),(1,0),(0,1) and (t,t) are concyclic, then t is equal to
-1
1
2
-2
The correct Answer is:B
To determine the value of t such that the points (0,0),(1,0),(0,1),(t,t) are concyclic, we can follow these steps:
Step 1: Understand the Concyclic Condition
The points are concyclic if they lie on the same circle. The general equation of a circle can be expressed as:
x2+y2+2gx+2fy+c=0
where g,f,c are constants.
Step 2: Substitute the Point (0,0)
Substituting (0,0) into the circle equation:
02+02+2g(0)+2f(0)+c=0
This simplifies to:
c=0
Step 3: Substitute the Point (1,0)
Now substitute (1,0):
12+02+2g(1)+2f(0)+c=0
Substituting c=0:
1+2g=0
From this, we find:
2g=−1⇒g=−12
Step 4: Substitute the Point (0,1)
Next, substitute (0,1):
02+12+2g(0)+2f(1)+c=0
Again substituting c=0:
1+2f=0
From this, we find:
2f=−1⇒f=−12
Step 5: Write the Circle Equation
Now we can write the equation of the circle using the values of g and f:
x2+y2−x−y=0
Step 6: Substitute the Point (t,t)
Now we substitute (t,t) into the circle equation:
t2+t2−t−t=0
This simplifies to:
2t2−2t=0
Factoring out 2t:
2t(t−1)=0
Step 7: Solve for t
Setting each factor to zero gives:
2t=0⇒t=0
or
t−1=0⇒t=1
Conclusion
Thus, the values of t are 0 and 1. Since the options provided are −1,1,2,−2, the correct answer is:
1
The points are concyclic if they lie on the same circle. The general equation of a circle can be expressed as:
x2+y2+2gx+2fy+c=0
where g,f,c are constants.
Substituting (0,0) into the circle equation:
02+02+2g(0)+2f(0)+c=0
This simplifies to:
c=0
Now substitute (1,0):
12+02+2g(1)+2f(0)+c=0
Substituting c=0:
1+2g=0
From this, we find:
2g=−1⇒g=−12
Next, substitute (0,1):
02+12+2g(0)+2f(1)+c=0
Again substituting c=0:
1+2f=0
From this, we find:
2f=−1⇒f=−12
Now we can write the equation of the circle using the values of g and f:
x2+y2−x−y=0
Now we substitute (t,t) into the circle equation:
t2+t2−t−t=0
This simplifies to:
2t2−2t=0
Factoring out 2t:
2t(t−1)=0
Setting each factor to zero gives:
2t=0⇒t=0
or
t−1=0⇒t=1
Thus, the values of t are 0 and 1. Since the options provided are −1,1,2,−2, the correct answer is:
1
Topper's Solved these Questions
- CIRCLESBOOK - OBJECTIVE RD SHARMA ENGLISHCHAPTER - CIRCLESEXERCISE - Section I - Solved Mcqs
108 Videos
- CIRCLESBOOK - OBJECTIVE RD SHARMA ENGLISHCHAPTER - CIRCLESEXERCISE - Section-I (Solved MCQs)
1 Videos
- CARTESIAN PRODUCT OF SETS AND RELATIONS BOOK - OBJECTIVE RD SHARMA ENGLISHCHAPTER - CARTESIAN PRODUCT OF SETS AND RELATIONS EXERCISE - Chapter Test
30 Videos
- COMPLEX NUMBERS BOOK - OBJECTIVE RD SHARMA ENGLISHCHAPTER - COMPLEX NUMBERS EXERCISE - Chapter Test
58 Videos
Similar Questions
If the points (2, 3), (0, 2), (4, 5) and (0, t) are concyclic, then t3+17 is equal to __________.
View SolutionIf the points (2, 0), (0, 1), (4, 5)and (0, c) are concyclic, then the value of c, is
View SolutionIf the points (2,0)(3,2)(5,4) and (0,t) are concylic, show that t=2 or 17.
View SolutionOn the xy plane where O is the origin, given points, A(1,0),B(0,1)andC(1,1). Let P,Q,andR be moving points on the line OA,OB,OC respectively such that ¯¯¯¯¯¯OP=45t¯¯¯¯¯¯¯¯¯(OA),¯¯¯¯¯¯OQ=60t¯¯¯¯¯¯¯¯¯(OB),¯¯¯¯¯¯OR=(1−t)¯¯¯¯¯¯¯¯¯(OC) with t>0. If the three points P,QandR are collinear then the value of t is equal to
A 1106
B 7187
C 1100
D none of these
View SolutionIf the points (a,0),(at12, 2at1)and at22, 2at2) are collinear, write the value of t1t2.
View SolutionIf x<0,thentan−1x is equal to
View SolutionIf f(x)=∫sinx0cos−1tdt+∫cosx0sin−1tdt,0<x<π2 then f(π/4) is equal to
View SolutionThe points (at21,2at1),(at22,2at2)and(a,0) will be collinear, if
View SolutionIf A(at2,2at),B(at2,−2at) and C(a,0) be any three points, show that 1AC+1BC is independent of t.
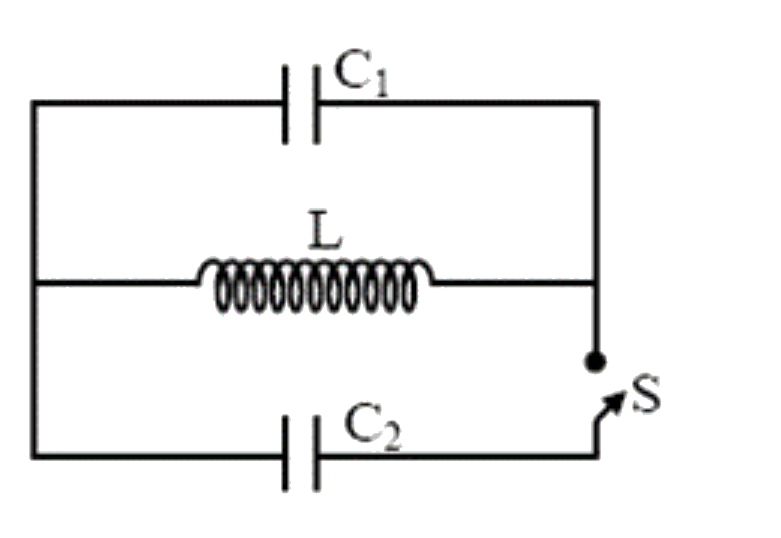
View SolutionAt the moment t = 0, when the charge on the capacitor C1 is zero, the switch is closed. If I0 be the current through inductor at t=0, then for t>0 (initally C2 is unchanged)
View Solution
