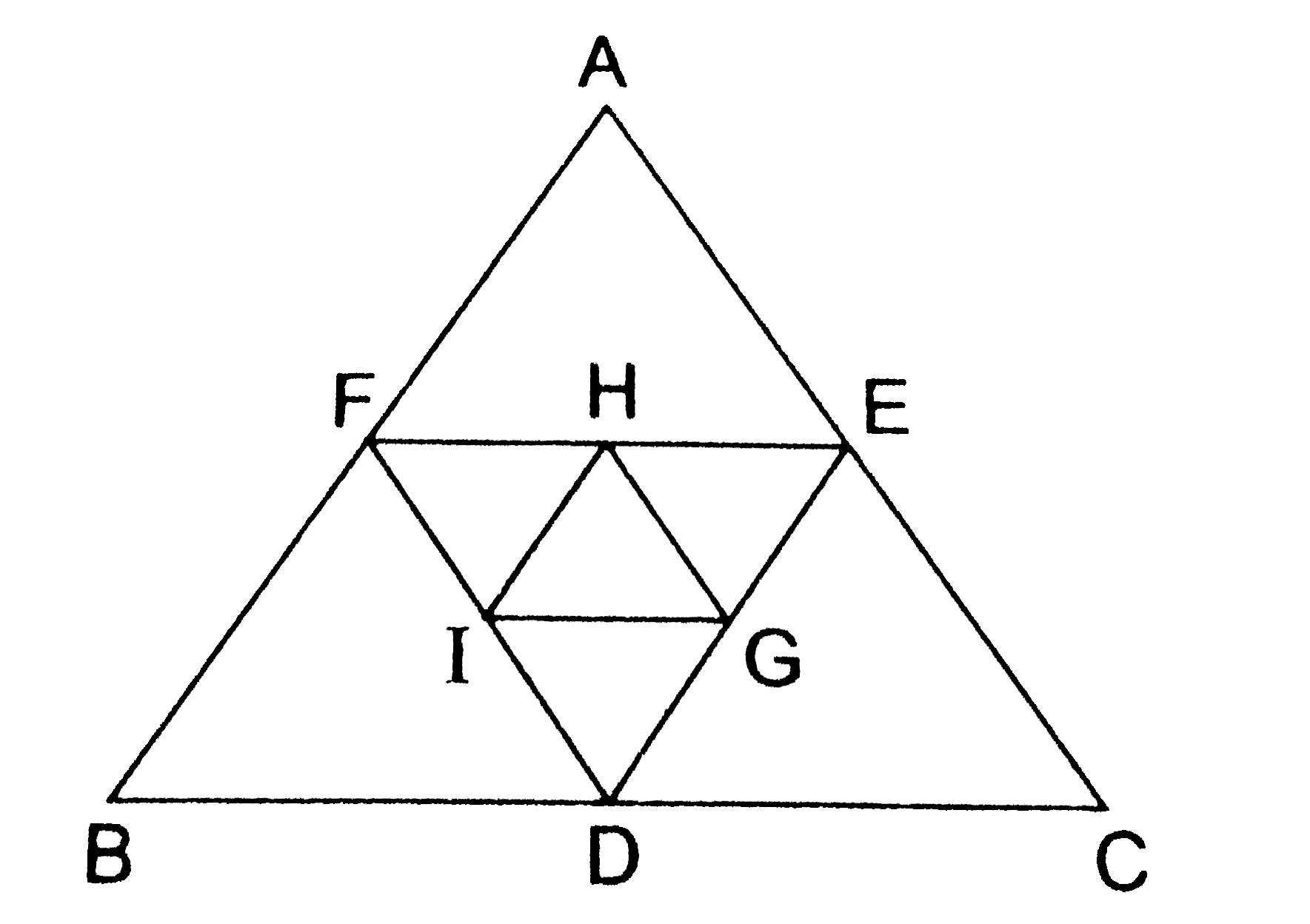
One side of an equilateral triangle is 18 cm. The mid-point of its sides are joined to form another triangle whose mid-points, in turn, are joined to form still another triangle. The process is continued indefinitely. Find the sum of the (i) perimeters of all the triangles. (ii) areas of all triangles.

Video Solution

Text Solution

Verified by Experts

Let $Δ A B C$ be the given triangle having each side 18 cm. Let D, E, F be the midpoints of BC, CA, AB respectively to form $Δ D E F$ . Let G, H, I be the midpoints of DE, EF and FD respectively to form $Δ G H I$ .
We continue this process indefinitely.
The sides of these triangle are 18 cm, 9 cm, $\frac{9}{2}$ cm, ..., and so on.
(i) Sum of the perimeters of all triangles so formed
$= 3 {18 + 9 + \frac{9}{2} + \frac{9}{4} + ... \infty} c m$
$= {3 \times \frac{a}{(1 - r)}} c m$ , where $a = 18$ and $r = \frac{9}{18} = \frac{1}{2}$
$= ⎧ ⎪ ⎪ ⎨ ⎪ ⎪ ⎩ 3 \times \frac{18}{(1 - \frac{1}{2})} ⎫ ⎪ ⎪ ⎬ ⎪ ⎪ ⎭ c m = (3 \times 36) c m = 108 c m$ .
(ii) Sum of the areas of all the triangles so formed
$= \frac{\sqrt{3}}{4} . {{(18)}^{2} + {(9)}^{2} + {(\frac{9}{2})}^{2} + {(\frac{9}{4})}^{2} + ... \infty} c m^{2}$
$= \frac{\sqrt{3}}{4} . {324 + 81 + \frac{81}{4} + \frac{81}{16} + ... \infty} c m^{2}$
$= \frac{\sqrt{3}}{4} . \frac{a}{(1 - r)} c m^{2}$ , where $a = 324$ and $r = \frac{81}{324} = \frac{1}{4}$
$= ⎧ ⎪ ⎪ ⎨ ⎪ ⎪ ⎩ \frac{\sqrt{3}}{4} \times \frac{324}{(1 - \frac{1}{4})} ⎫ ⎪ ⎪ ⎬ ⎪ ⎪ ⎭ c m^{2} = 108 \sqrt{3} c m^{2}$ .

Updated on:21/07/2023