Orthocenter and circumcenter of a DeltaABC are (a,b)and(c,d) , respectively. If the coordinates of the vertex A are (x1,y1), then find the coordinates of the middle point of BC.
Given are the orthocentre H(a,b) and the circumcentre O(c,d).

∴ Centroid, G=(2c+a2+1,2d+b2+1)≡(2c+a3,2d+b3)
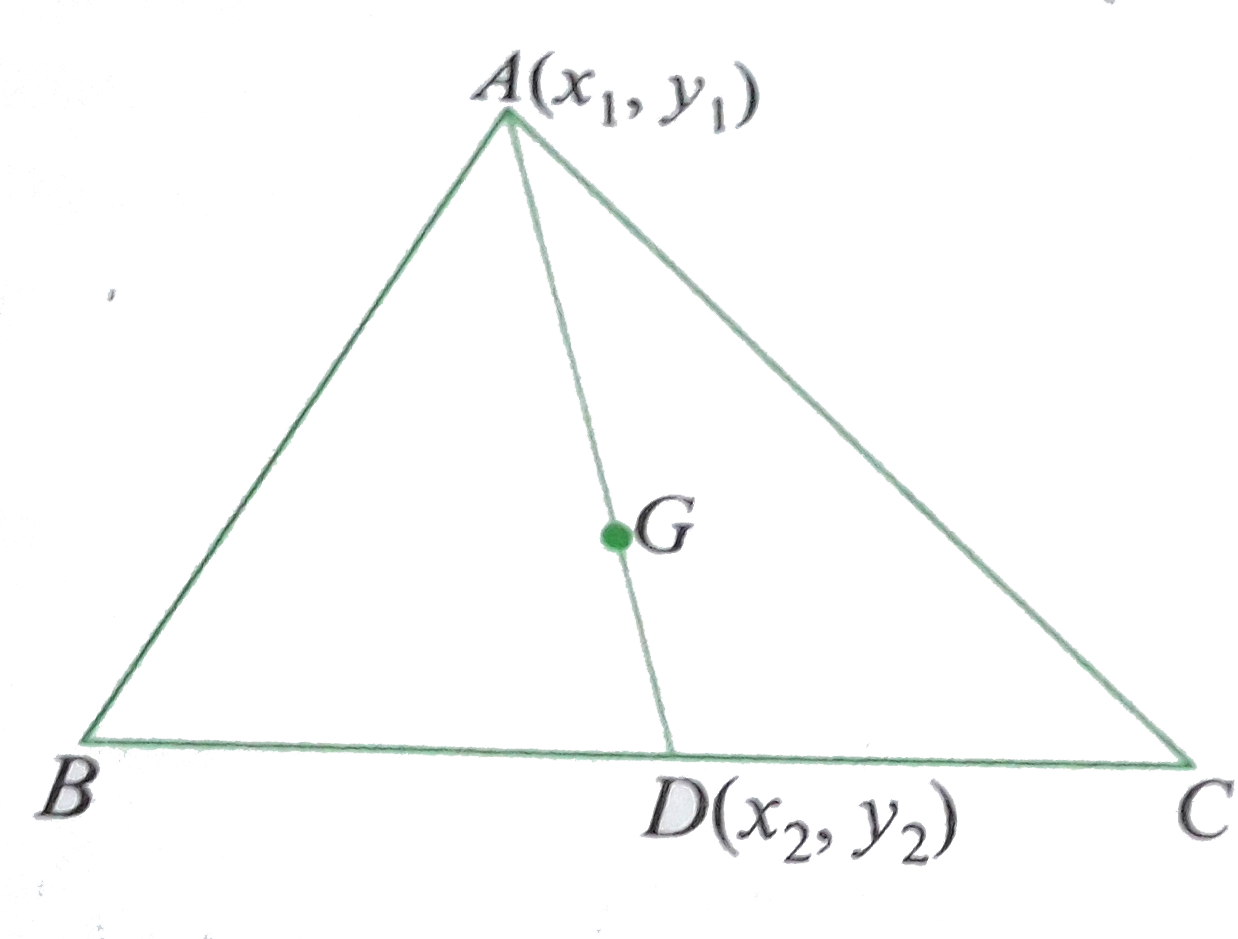
Now, centroid G divides AD in the ratio 2:, where D is the midpoint of BC.
∴2c+a3=2x2+x13
and 2d+b3=2y2+y−13
∴x2=2c+a−x12,y2=2d+b−y12
Topper's Solved these Questions
- COORDINATE SYSYEM BOOK - CENGAGECHAPTER - COORDINATE SYSYEM EXERCISE - Exercise 1.1
6 Videos
- COORDINATE SYSYEM BOOK - CENGAGECHAPTER - COORDINATE SYSYEM EXERCISE - Exercise 1.2
8 Videos
- COORDINATE SYSTEMBOOK - CENGAGECHAPTER - COORDINATE SYSTEMEXERCISE - Multiple Correct Answers Type
2 Videos
- CROSS PRODUCTS BOOK - CENGAGECHAPTER - CROSS PRODUCTS EXERCISE - DPP 2.2
13 Videos
Similar Questions
Orthocenter and circumcenter of a DeltaABC are (a,b)and(c,d) , respectively. If the coordinates of the vertex A are (x1,y1), then find the coordinates of the middle point of BC.
View SolutionABC is an isosceles triangle. If the coordinates of the base are B(1, 3) and C(-2, 7). The coordinates of vertex A can be
View Solution
Knowledge Check
ABC is an isosceles triangle. If the coordinates of the base are B(1,3) and C(-2,7), the coordinates of vertex A can be
A(1,6)B(−1/2,5)C(−5/6,6)Dnone of theseABC is an isosceles triangle. If the coordinates of the base are B(1,3) and C(-2,7), the coordinates of vertex A can be
A(1,6)B(−12,5)C(56,6)D(−7,18)If the coordinates of the centroid and a vertex of an equilaterqal triangle are (1,1) and (1,2) respectively, then the coordinates of another vertex, are
A(2−√32,−12)B(2+3√32,−12)C(2+√32,−12)Dnone of these
Find the coordinates of points A, B, C, D in Figure.

View SolutionThe centroid of a triangle ABC is at the point (1,1,1). If the coordinates of A and B are (3,-5,7) and (-1,7,-6) respectively, find the coordinates of the point C.
View SolutionThe origin is the centroid of a triangle ABC is at the point G(1,1,1). If the coordinates of A and B are (3,-5,7) an (-1,7,-6) respectively, then find the coordinates of the point C.
View SolutionIn the adoining figure if the coordinates of point P are (a,b,c) write the coordinates of A,B,C,D,E and F.
View SolutionIn the following figure, if the coordinates of P are (a,b,c) then the coordinates of A,B and C are respectively
View Solution
