Orthocenter and circumcenter of a triangleABC are (a,b)and(c,d) , respectively. If the coordinates of the vertex A are (x1,y1), then find the coordinates of the middle point of BC.
Given are the orthocentre H(a,b) and the circumcentre O(c,d).

∴ Centroid, G=(2c+a2+1,2d+b2+1)≡(2c+a3,2d+b3)
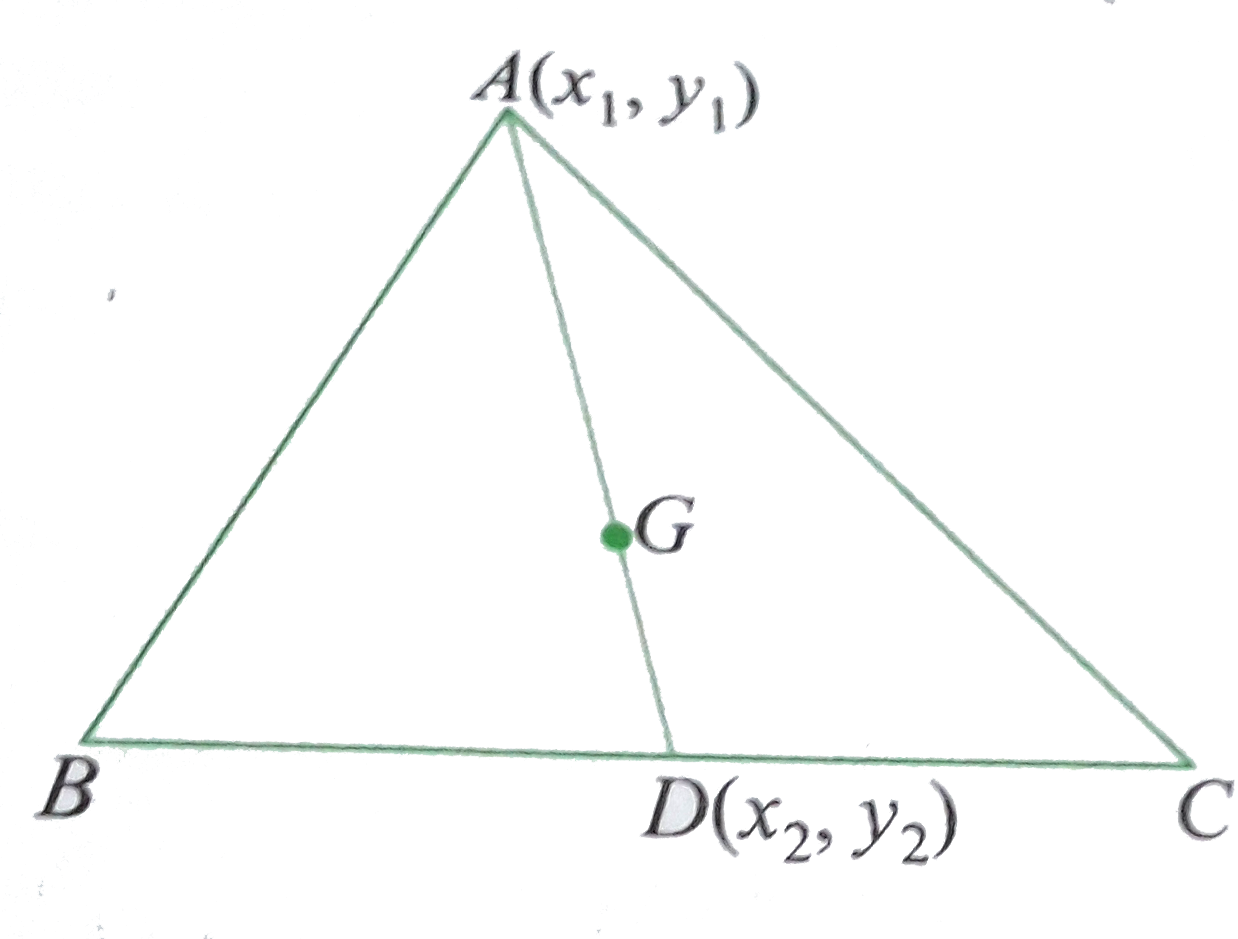
Now, centroid G divides AD in the ratio 2:, where D is the midpoint of BC.
∴2c+a3=2x2+x13
and 2d+b3=2y2+y−13
∴x2=2c+a−x12,y2=2d+b−y12
Topper's Solved these Questions
- COORDINATE SYSYEM BOOK - CENGAGE ENGLISHCHAPTER - COORDINATE SYSYEM EXERCISE - Illustration1.36
1 Videos
- COORDINATE SYSYEM BOOK - CENGAGE ENGLISHCHAPTER - COORDINATE SYSYEM EXERCISE - Illustration1.37
1 Videos
- COORDINATE SYSYEM BOOK - CENGAGE ENGLISHCHAPTER - COORDINATE SYSYEM EXERCISE - Illustration1.34
1 Videos
- COORDINATE SYSTEMBOOK - CENGAGE ENGLISHCHAPTER - COORDINATE SYSTEMEXERCISE - Multiple Correct Answers Type
2 Videos
- CROSS PRODUCTS BOOK - CENGAGE ENGLISHCHAPTER - CROSS PRODUCTS EXERCISE - DPP 2.2
13 Videos
Similar Questions
Orthocenter and circumcenter of a ΔABC are (a,b)and(c,d) , respectively. If the coordinates of the vertex A are (x1,y1), then find the coordinates of the middle point of BC.
View SolutionABC is an isosceles triangle. If the coordinates of the base are B(1,3) and C(−2,7) , the coordinates of vertex A
View SolutionThe centroid of a triangle ABC is at the point (1,1,1). If the coordinates of A and B are (3,5,7)and (1,7,6), respectively, find the coordinates of the point C.
View SolutionABC is an isosceles triangle. If the coordinates of the base are B(1, 3) and C(-2, 7). The coordinates of vertex A can be
View SolutionThe centroid of a triangle ABC is at the point (1,1,1). If the coordinates of A and B are (3,-5,7) and (-1,7,-6) respectively, find the coordinates of the point C.
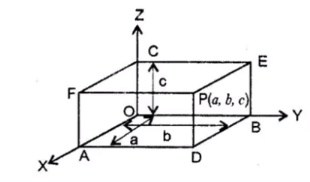
View SolutionIn the adoining figure if the coordinates of point P are (a,b,c) write the coordinates of A,B,C,D,E and F.
View SolutionABCD is parallelogram. If the coordinates of A,B,C are (−2,−1),(3,0) and (1,−2) respectively, find the coordinates of D.
View SolutionABCD is parallelogram. If the coordinates of A,B,C are (−2,−1),(3,0) and (1,−2) respectively, find the coordinates of D.
View SolutionThe equations of the perpendicular bisectors of the sides ABandAC of triangle ABC are x−y+5=0 and x+2y=0 , respectively. If the point A is (1,−2) , then find the equation of the line BC.
View SolutionThe equations of the perpendicular bisectors of the sides ABandAC of triangle ABC are x−y+5=0 and x+2y=0 , respectively. If the point A is (1,−2) , then find the equation of the line BC.
View Solution
