Orthocenter and circumcenter of a ΔABC are (a,b)and(c,d) , respectively. If the coordinates of the vertex A are (x1,y1), then find the coordinates of the middle point of BC.
To find the coordinates of the midpoint of line segment BC in triangle ABC, given the orthocenter and circumcenter, we can follow these steps:
1. Identify Given Points:
- Orthocenter O is given as (a,b).
- Circumcenter C is given as (c,d).
- Vertex A is given as (x1,y1).
2. Use the Relationship Between Orthocenter, Circumcenter, and Centroid:
- The centroid G of triangle ABC can be expressed using the coordinates of the vertices A, B, and C:
G=(x1+x2+x33,y1+y2+y33)
- The centroid divides the line segment joining the orthocenter O and circumcenter C in the ratio 2:1.
3. Apply Section Formula:
- Using the section formula, we can find the coordinates of the centroid G:
G=(2c+a3,2d+b3)
4. Set Up Equations for Centroid:
- Equating the two expressions for G:
x1+x2+x33=2c+a3
y1+y2+y33=2d+b3
5. Multiply Through by 3:
- This gives us two equations:
x1+x2+x3=2c+a
y1+y2+y3=2d+b
6. Express Coordinates of B and C:
- Let the coordinates of points B and C be (x2,y2) and (x3,y3) respectively.
- Rearranging gives:
x2+x3=(2c+a)−x1
y2+y3=(2d+b)−y1
7. Find Midpoint of BC:
- The coordinates of the midpoint M of segment BC are given by:
M=(x2+x32,y2+y32)
- Substitute the expressions for x2+x3 and y2+y3:
M=((2c+a)−x12,(2d+b)−y12)
Final Answer:
The coordinates of the midpoint of BC are:
M=(2c+a−x12,2d+b−y12)
- Orthocenter O is given as (a,b).
- Circumcenter C is given as (c,d).
- Vertex A is given as (x1,y1).
- The centroid G of triangle ABC can be expressed using the coordinates of the vertices A, B, and C:
G=(x1+x2+x33,y1+y2+y33)
- The centroid divides the line segment joining the orthocenter O and circumcenter C in the ratio 2:1.
- Using the section formula, we can find the coordinates of the centroid G:
G=(2c+a3,2d+b3)
- Equating the two expressions for G:
x1+x2+x33=2c+a3
y1+y2+y33=2d+b3
- This gives us two equations:
x1+x2+x3=2c+a
y1+y2+y3=2d+b
- Let the coordinates of points B and C be (x2,y2) and (x3,y3) respectively.
- Rearranging gives:
x2+x3=(2c+a)−x1
y2+y3=(2d+b)−y1
- The coordinates of the midpoint M of segment BC are given by:
M=(x2+x32,y2+y32)
- Substitute the expressions for x2+x3 and y2+y3:
M=((2c+a)−x12,(2d+b)−y12)
The coordinates of the midpoint of BC are:
M=(2c+a−x12,2d+b−y12)
Topper's Solved these Questions
Similar Questions
Orthocenter and circumcenter of a triangleABC are (a,b)and(c,d) , respectively. If the coordinates of the vertex A are (x1,y1), then find the coordinates of the middle point of BC.
View SolutionABC is an isosceles triangle. If the coordinates of the base are B(1,3) and C(−2,7) , the coordinates of vertex A
View SolutionABC is an isosceles triangle. If the coordinates of the base are B(1, 3) and C(-2, 7). The coordinates of vertex A can be
View SolutionThe centroid of a triangle ABC is at the point (1,1,1). If the coordinates of A and B are (3,5,7)and (1,7,6), respectively, find the coordinates of the point C.
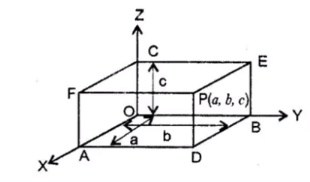
View SolutionIn the adoining figure if the coordinates of point P are (a,b,c) write the coordinates of A,B,C,D,E and F.
View SolutionThe centroid of a triangle ABC is at the point (1,1,1). If the coordinates of A and B are (3,-5,7) and (-1,7,-6) respectively, find the coordinates of the point C.
View SolutionABCD is parallelogram. If the coordinates of A,B,C are (−2,−1),(3,0) and (1,−2) respectively, find the coordinates of D.
View SolutionABCD is parallelogram. If the coordinates of A,B,C are (−2,−1),(3,0) and (1,−2) respectively, find the coordinates of D.
View SolutionABC is an isosceles triangle. If the coordinates of the base are B(1,3) and C(−2,7) , the coordinates of vertex A can be (1,6) (b) (−12,5) (56,6) (d) none of these
View SolutionABCD is a parallelogram. If the coordinates of A, B, C are (2,3), (1,4)and (0,−2) respectively, find the coordinates of D.
View Solution
