P and Q are the mid-points of the sides CA and CB respectively of a ΔABC, right angled at C, then find :
(i) 4AC2+BC2
(ii) 4BC2+AC2
(iii) 4(AQ2+BP2)
(i)(ii)(iii)4AQ24BP25AB2
(i)(ii)(iii)5AQ25BP24AB2
(i)(ii)(iii)4AQ25BP25AB2
(i)(ii)(iii)5AQ24BP24AB2
The correct Answer is:A
To solve the problem step by step, we will analyze each part of the question separately.
Given:
- Triangle ABC is right-angled at C.
- P and Q are the midpoints of sides CA and CB respectively.
(i) Find 4AC2+BC2
1. Identify the right triangle: In triangle ACQ, since C is the right angle, we can apply the Pythagorean theorem.
AQ2=AC2+CQ2
2. Express AC2: Rearranging the equation gives us:
AC2=AQ2−CQ2
3. Express BC: Since Q is the midpoint of CB, we can express BC in terms of CQ:
BC=2CQ
4. Substitute BC: Now substituting BC into the equation:
4AC2+BC2=4(AQ2−CQ2)+(2CQ)2
5. Simplify the equation:
=4AQ2−4CQ2+4CQ2
The −4CQ2 and +4CQ2 cancel out:
=4AQ2
Final Result for (i):
4AC2+BC2=4AQ2
- Triangle ABC is right-angled at C.
- P and Q are the midpoints of sides CA and CB respectively.
AQ2=AC2+CQ2
4AC2+BC2=4AQ2
Topper's Solved these Questions
Similar Questions
P and Q are the mid point of the sides CA and CB respectively of a triangle ABC, right angled at C. then, find the value of 4 (AQ2+BP2).
View SolutionP and Q are the mid-points of the sides CA and CB respectively of a △ABC , right angled at C, prove that. (i) 4AQ2=4AC2+BC2 (ii) 4BP2=4BC2+AC2
View Solution
Knowledge Check
- Question 1 - Select One
P and Q are the mid-points of the sides AB and BC, respectively, of ΔABC, right angled at B. Then:
AAQ2+CP2=AC2BAQ2+CP2=45AC2CAQ2+CP2=43AC2DAQ2+CP2=54AC2 - Question 2 - Select One
P and Q are points on the sides CA and CB respectively of ABC , right angled at C . Prove that AQ2+BP2=AB2+PQ2 .
ABC2+PQ2BAB2+PC2CAB2+PQ2DBC2+AC2 - Question 3 - Select One
L and M are the mid points of AB and BC respectively of ΔABC , right angled at B . 4LC2=
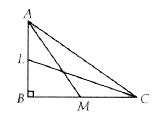 AAB2+4BC2BBC2+4AB2CAC2+4AB2DNone of these
AAB2+4BC2BBC2+4AB2CAC2+4AB2DNone of these
P and Q are points on the sides CA and CB respectively of ABC, right-angled at C. Prove that AQ2+BP2=AB2+PQ2.
View SolutionP and Q are the points on sides AB and AC respectively of a ΔABC , such that PQ||BC .If AP∣PB=2:3 and AQ=4 cm , then the length of AC is ….. Cm .
View SolutionIn a right triangle ABC , right angled at C, P and Q are the points of the sides CA and CB respectively , which divide these sides in the ratio 2:1 Prove that
9BP2=9BC2+4AC2View SolutionIn a right triangle ABC , right angled at C, P and Q are the points of the sides CA and CB respectively , which divide these sides in the ratio 2:1 Prove that
9AQ2=9AC2+4BC2View SolutionIn a right triangle ABC , right angled at C, P and Q are the points of the sides CA and CB respectively , which divide these sides in the ratio 2:1 Prove that
9(AQ2+BP2)=13AB2View Solution
