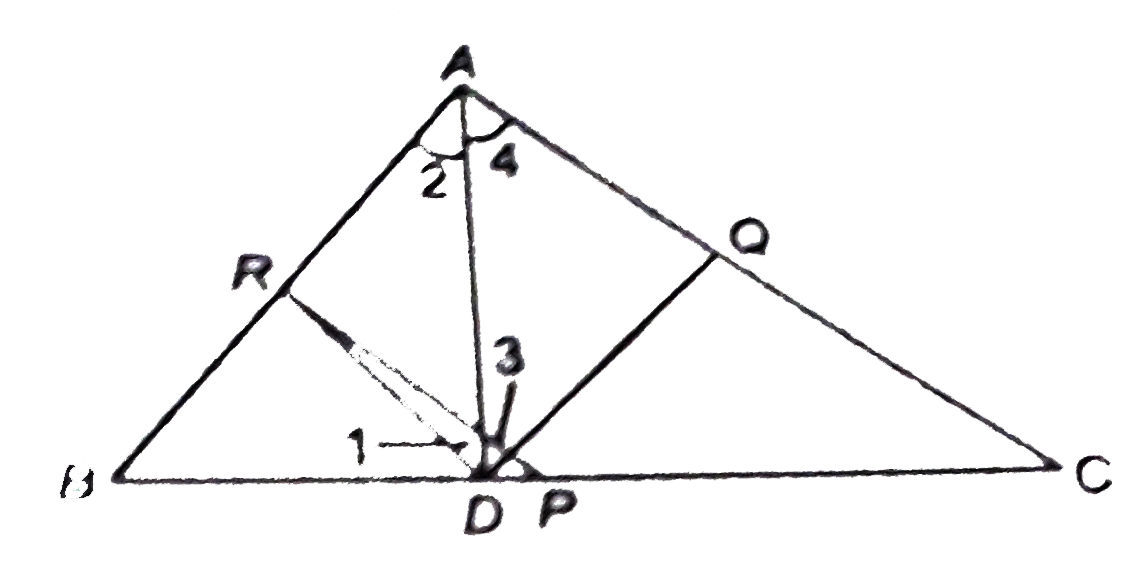
P, Q and R are, respectively, the mid points of sides BC, CA and AB of a triangle ABC
We have to prove that R,D,P and Q are concyclic.
Join RD, QD,PR and PQ.
Since, RP joins R and P, the mid-point of AB and BC.
∴RP| |AC (mid-point theorem)
Similarly, PQ| |AC
Therefore, ARPQ is parallelogram.
So, ∠RAQ=∠RPQ (opposite angles of a parallelogram.....(1)
Since, ABD is a right-angled triangle and DR is a median.
∴RA=DR and ∠1=∠2 ......(2)
Similarly , ∠3=∠4........(3)
Adding eqs. (2) and (3) , we get
∠1+∠3=∠2+∠4
⇒∠RDQ=∠RAQ
=∠RPQ (proved above)
Hence R,D,P and Q are concyclic.
(∵∠D and ∠P are subtended by RQ on the same side of it.)
Topper's Solved these Questions
- CIRCLE BOOK - NAGEEN PRAKASHAN ENGLISHCHAPTER - CIRCLE EXERCISE - Exercise 10a
22 Videos
- CIRCLE BOOK - NAGEEN PRAKASHAN ENGLISHCHAPTER - CIRCLE EXERCISE - Exercise 10b
19 Videos
- AREA OF PARALLELOGRAMS AND TRIANGLESBOOK - NAGEEN PRAKASHAN ENGLISHCHAPTER - AREA OF PARALLELOGRAMS AND TRIANGLESEXERCISE - Revision Exercise (long Answer Question)
5 Videos
- CO-ORDINATE GEOMETRY BOOK - NAGEEN PRAKASHAN ENGLISHCHAPTER - CO-ORDINATE GEOMETRY EXERCISE - Exercise
8 Videos
Similar Questions
P,Q and R are, respectively, the mid-points of sides BC,CA and AB of a triangle ABC , PR and BQ meet at X.CR and PQ meet at Y . Prove that XY=14BC.
View SolutionIn Figure, D,E and F are, respectively the mid-points of sides BC,CA and AB of an equilateral triangle ABC . Prove that DEF is also an equilateral triangle.
View SolutionIn Figure, D,E and F are, respectively the mid-points of sides BC,CA and AB of an equilateral triangle ABC . Prove that DEF is also an equilateral triangle.
View SolutionIn △ABC, D, E and F are, respectively, the mid-points of BC, CA and AB . If the lengths of side AB, BC and CA are 7cm, 8cm, and 9cm, respectively, find the perimeter of △DEF.
View SolutionIn Figure, BE⊥AC, AD is any line from A → BC intersecting BE in H.P, Q and R are respectively the mid-points of AH, AB and BC. Prove that ∠PQR=900
View SolutionIn a triangle, P, Q and R are the mid-points of sides BC, CA and AB respectively. If AC=21 cm, BC=29cm and AB=30cm, find the perimeter of the quadrilateral ARPQ
View SolutionGiven ABC , lines are drawn through A, B and C parallel respectively to the sides BC, CA and AB, forming triangle P Q R . Show that BC=1/2QR.
View SolutionGiven △ABC , lines are drawn through A, B and C parallel respectively to the sides BC, CA and AB, forming △PQR.(Figure). Show that BC=12QR.
View SolutionIf E, F, G and H are respectively the mid-points of the sides of a parallelogram ABCD, Show that ar(EFGH)=12ar (ABCD)
View SolutionIn △ABC, P and Q are respectively the mid-points of AB and BC and R is the mid-point of AP. Prove that: ar (△RQC)=38 ar (△ ABC).
View Solution
