P, Q, R and S are respectively the mid-points of the sides AB, BC, CD and DA of a quadrilateral ABCD such that AC ⊥ BD. Prove that PQRS is a rectangle.
Vertices as midpoint of quadrilateral from parallelogram
∠ABD
PS||BD
BD⊥AC
PS⊥AC
∠ABC
PQ||AC
AC⊥BD
PQ⊥BD
PQ⊥PS
∠SPQ=900
Topper's Solved these Questions
Similar Questions
P, Q , R and S are respectively the mid-points of the sides AB, BC, CD and DA of a quadrilateral ABCD in which AC = BD. Prove that PQRS is a rhombus.
View SolutionP, Q, R and S are respectively the mid-points of sides AB, BC, CD and DA of quadrilateral ABCD in which AC=BD and AC⊥BD. Prove that PQRS is a square.
View SolutionABCD is a rhombus and P, Q, R and S are wthe mid-points of the sides AB, BC, CD and DA respectively. Show that the quadrilateral PQRS is a rectangle.
View SolutionIf the sides of a quadrilateral ABCD touch a circle prove that
AB+CD=BC+AD.
View SolutionP,Q,R and S are the mid points of sides AB,BC , CD and DA respectively of rhombus ABCD. Show that PQRS is a rectangle.
Under what conditions will PQRS be a square ?
View SolutionP and Q are the mid-point of the opposite sides AB and CD of a parallelogram ABCD. AQ intersects DP at S and BQ intersects CP at R. Show that PQRS is a parallelogram.

View SolutionIn figure, P is the mid-point of side BC of a parallelogram ABCD such that ∠BAP=∠DAP. Prove that AD = 2CD.
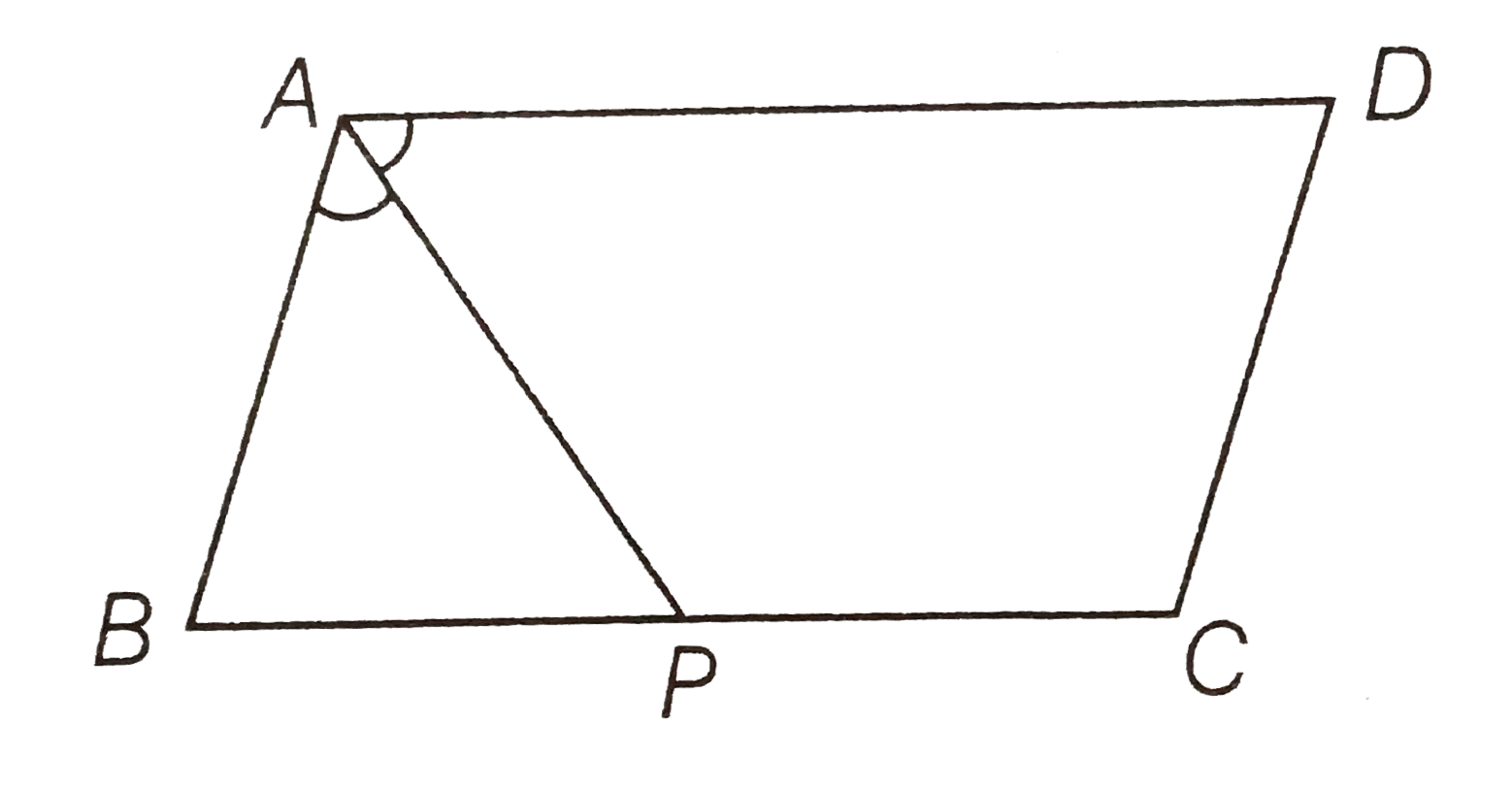
View SolutionShow that in a quadrilateral ABCD AB+BC+CD+DA>AC+BD
View SolutionABCD is a quadrilateral in which P, Q, R and S are mid-points of the sides AB, BC, CD and DA. AC is a diagonal. Show that : (i) SR ∣∣ AC and SR=12AC (ii) PQ=SR (iii) PQRS is a parallelogram
View SolutionABCD is a rectangle and P, Q, R and S are mid-points of the sides AB, BC, CD and DA respectively. Show that the quadrilateral PQRS is a rhombus.
View Solution
