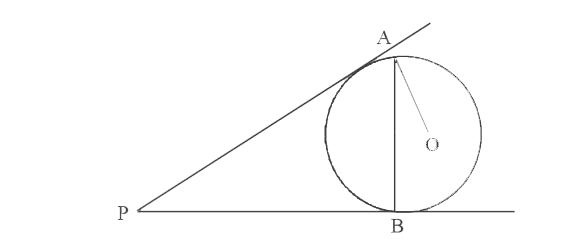
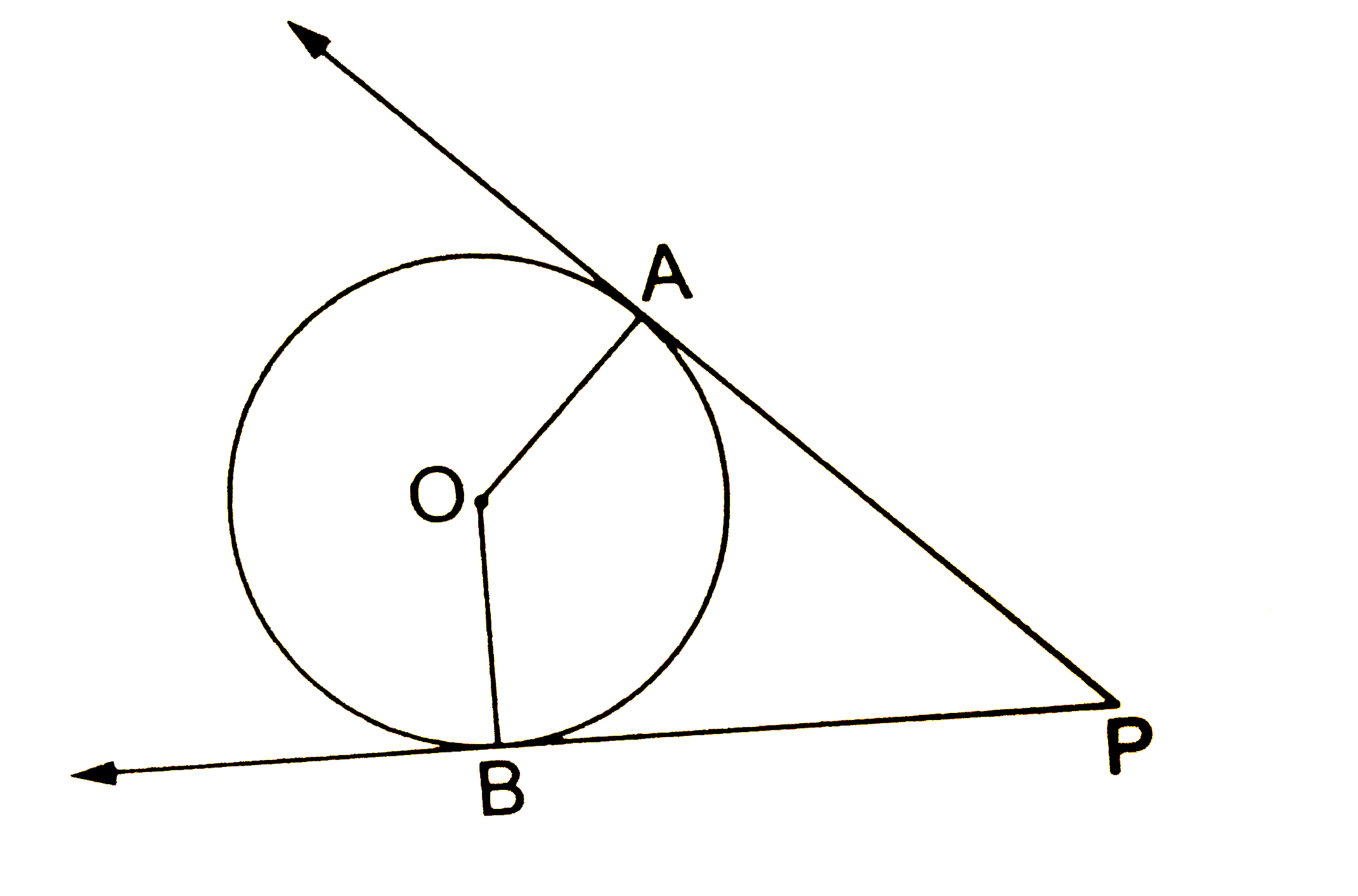
PA and PB are tangents to the circle with centre O from an external point P, touching the circle at A and B respectively. Show that the quadrilateral AOBP is cyclic.
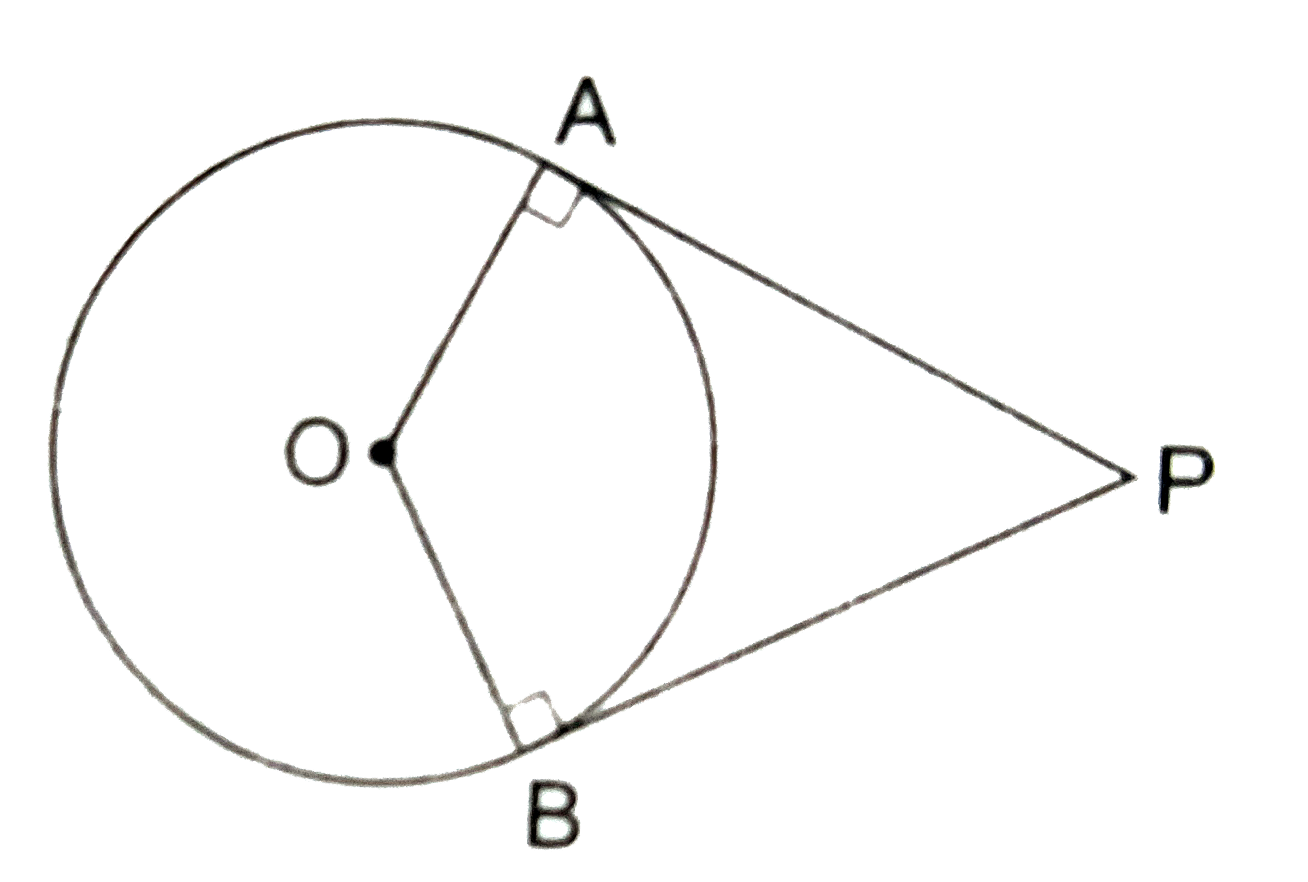
GIVEN PA and PB are tangents to the circle with centre O from an external point P.
TO PROVE Quadrilateral AOBP is cyclic.
PROOF We know that the tangent at any point of a circle is perpendicular to radius through the point of contact
∴PA⊥OA, i.e., ∠OAP=90∘.........(i)
and PB⊥OB, i.e., ∠OBP=90∘..........(ii)
Now, the sum of all the angles of a quadrilateral is 360∘.
∴∠AOB+∠OAP+∠APB+∠OBP=360∘
⇒∠AOB+∠APB=180∘ [using (i) and (ii)]
∴ quadrilateral OAPB is cyclic [since both pairs of opposite angles have the sum 180∘]
Topper's Solved these Questions
- BOOK - RS AGGARWALCHAPTER - CIRCLESEXERCISE - Exercise 8A16videos
CIRCLES
- BOOK - RS AGGARWALCHAPTER - CIRCLESEXERCISE - Exercise 8B15videos
CIRCLES
- BOOK - RS AGGARWALCHAPTER - ARITHMETIC PROGRESSIONEXERCISE - Multiple Choice Questions (Mcq)30videos
ARITHMETIC PROGRESSION
- BOOK - RS AGGARWALCHAPTER - CONSTRUCTIONSEXERCISE - Test Yourself10videos
CONSTRUCTIONS
Similar Questions
Knowledge Check
- Question 1 - Select One
Two tangents PA and PB are drawn to a circle with centre O from an external point P. If ∠OAB=30∘, then ∠APB is:
केंद्र O वाले वृत्त पर एक बाहरी बिंदु P से दो स्पर्श रेखाएँ PA तथा PB खींची जाती हैं | यदि ∠OAB=30∘ है, तो ∠APB का मान क्या होगा ?A15∘B30∘C120∘D60∘ - Question 2 - Select One
PA and PB are tangents to a circle with centre O, from a point P outside the circle and A and B are points on the circle. If ∠APB=30∘, then ∠OAB is equal to :
AA) 40∘BB) 15∘CC) 50∘DD) 25∘ - Question 3 - Select One
PA and PB are two tangents to a circle with centre O, from a point P outside the circle. A and B are points on the circle. If ∠APB=40∘, then ∠OABis equal to:
A40∘B20∘C50∘D25∘
PA and PB are tangents to a circle with centre O from point P. OP is equal to the diameter of the circle. Prove that ABP is equilateral triangle,
View SolutionPA and PB are tangents to a circle with centre 0, from a point P outside the circle, and A and B are point on the circle. If ∠APB=30∘, then ∠OAB is equal to:
View SolutionPA and PB are two tangents to a circle with centre O, from a point P outside the circle. A and B are points on the circle. If ∠APB=100∘ , then OAB is equal to:
View SolutionPA and PB are two tangents to a circle with centre O, from a point P outside the circle . A and B are point P outside the circle . A and B are point on the circle . If ∠PAB=47∘ , then ∠OAB is equal to :
View SolutionPA and PB are two tangents to a circle with centre 0. from a point P outside the circle. A and B are points on the circle. If ∠APB=70∘ then ∠OAB is equal to:
View Solution