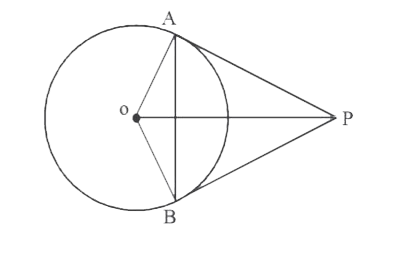
PA and PB are tangents to a circle with centre O from point P. OP is equal to the diameter of the circle. Prove that ABP is equilateral triangle,
Diameter=2r
OP=2r
OC+CP=2r
CP=2r-r=r
OC=CP
C is MP of OP
∠OAP is right agled triangle
OP is hyperbola
OA=AC=OC=r
∠AOC=600
∠AOP+∠APO=900
∠APO=90−60=300
∠APB=600
∠PAB=∠PBA
∠PAB+∠PBA+∠APB=1800
2∠PAB=1200
∠PAB=600=∠PBA
∠PAB is an equilateral triangle.
Similar Questions
In the given fig. OP is equal to the diameter of the circle with centre O. Prove that ΔABP is an equilateral triangle.
View SolutionTwo tangents PA and PB are drawn to circle with centre O from an external point P. Prove that ∠APB=2∠OAB
View SolutionFrom a point P outside a circle, with centre O, tangents PA and PB are drawn. Prove that
(i) ∠AOP=∠BOP
(ii) OP is the ⊥ bisector of chord AB.
View SolutionFrom a point P, two tangents PA and PB are drawn to a circle with centre O and radius r. If OP=2r, show that △APB is equilateral.

View Solutionएक वृत्त C(O, r) के बाह्य बिंदु P से वृत्त पर PA और PB दो स्पर्श रेखाएँ इस प्रकार खींची गई हैं कि ∠APB=120∘है। सिद्ध करो कि OP=2AP
View SolutionFrom a point P, two tangents PA and PB are drawn to a circle with centre O. If OP is equal to diameter of the circle then ∠APB is___
View SolutionO is the centre of a circle. There is a point P in the region of the circle. If PA = PB = PC where A, B and C are points on the circumference of the circle, then OP must be equal to :
View SolutionFrom a point P, two tangents PA and PB are drawn to a circle with centre O. If OP is equal to diameter of the circle, then ∠APBis
View Solution
