Parallelogram ABCD and rectangle ABEF are on the same base AB and have equal areas. Show that the perimeter of the parallelogram is greater than that of the rectangle. Solution in Kannada
Step by step video & image solution for Parallelogram ABCD and rectangle ABEF are on the same base AB and have equal areas. Show that the perimeter of the parallelogram is greater than that of the rectangle. by Maths experts to help you in doubts & scoring excellent marks in Class 9 exams.
Updated on:21/07/2023Topper's Solved these Questions
- AREA OF PARALLELOGRAMS AND TRIANGLESBOOK - SUBHASH PUBLICATIONCHAPTER - AREA OF PARALLELOGRAMS AND TRIANGLESEXERCISE - EXERCISE 11.3
8 Videos
- APPENDIX ABOOK - SUBHASH PUBLICATIONCHAPTER - APPENDIX AEXERCISE - EXERCISE A 1.4
10 Videos
- CIRCLESBOOK - SUBHASH PUBLICATIONCHAPTER - CIRCLESEXERCISE - EXERCISE 12.6
7 Videos
Similar Questions
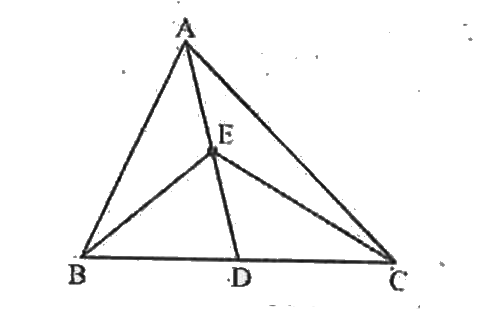
In the figure 11.23, E is any point on median AD of a ΔABC. Show that ar (ABE) = ar (ACE).
View SolutionFind counter - examples to disprove the following statements :
If the corresponding angles in two triangles are equal, then the triangles are congruent.
View SolutionProve that the line of centres of two intersecting circles subtends equal angles at the two points of intersection.
View SolutionParallelogram ABCD and rectangle ABEF are on the same base AB and have equalareas. Show that the perimeter of the parallelogram is greater than that of the rectangle.
View Solutionसमांतर चतुर्भुज ABCD और आयत ABEF एक ही आधार पर स्थित है और उनके क्षेत्रफल बराबर है । दर्शाइए की समांतर चतुर्भुज का परिमाप आयत के परिमाप से अधिक है ।
View Solutionसमांतर चतुर्भुज ABCD और आयत ABEF एक ही आधार पर स्तिथ है और उनके क्षेत्रफल बराबर है। दर्शाइए कि समांतर चतुर्भुज का परिमाण आयत के परिमाप से अधिक है।
View Solutionएक आयत व एक समांतर चतुर्भुज का क्षेत्रफल बराबर व आधार उभयनिष्ठ है। सिद्ध कीजिए कि आयत का परिमाप समांतर चतुर्भुज के परिमाप से कम होता है।
View Solutionसमान्तर चतुर्भुज ABCD और आयत ABEF एक ही आधार पर स्थित है और उनके क्षेत्रफल बराबर है। दर्शाइए कि समान्तर चतुर्भुज का परिमाप आयत के परिमाप आयत के परिमाप से अधिक है।
View SolutionParallelogram ABCD and rectangle ABEF are on the base AB and have equal areas. Show that the perimeter of the parallelogram is greater than that of the rectangle.
View Solutionಸಮಾಂತರ ಚತುರ್ಭುಜ ABCD ಮತ್ತು ABEF ಆಯತಗಳು AB ಪಾದದ ಮೇಲಿದ್ದು ವಿಸ್ತೀರ್ಣಗಳು ಸಮನಾಗಿವೆ. ಆದರೆ ಸಮಾಂತರ ಚತುರ್ಭುಜದ ಸುತ್ತಳತೆಯು ಆಯತದ ಸುತ್ತಳತೆಗಿಂತ ಹೆಚ್ಚಾಗಿರುತ್ತದೆ ಎಂದು ಸಾಧಿಸಿ.
View SolutionIf a rectangle and a parallelogram are equal in area and have the same base and are situated on the same side, then the ratio of perimeter of rectangle and that of parallelogram is k, then k is :
View SolutionParallelogram ABCD and rectangle ABEF are on the same base AB and have equal areas. Show that the perimeter of the parallelogram is greater than that of the rectangle.
View SolutionParallelogram ABCD and rectangle ABEF have the same base AB and also have equal areas. Show that the perimeter of the parallelogram is greater than that of the rectangle.
View SolutionParallelogram ABCD and rectangle ABEF are on the same base AB and have equal areas. Show that the perimeter of the parallelogram is greater than that of the rectangle.
View SolutionIn Fig.
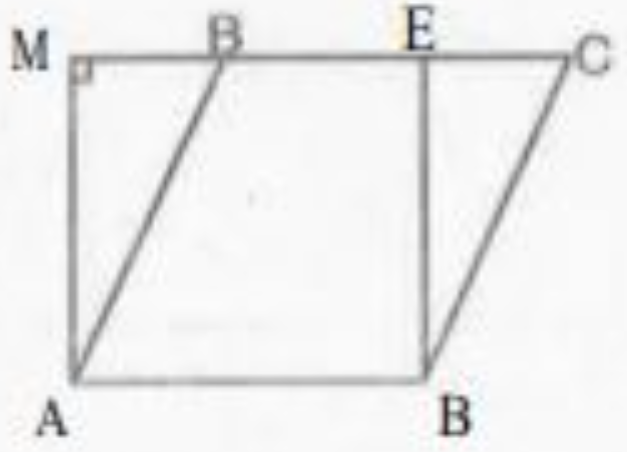 if parallelogram ABCD and rectangle ABEF are of equal area, then :
if parallelogram ABCD and rectangle ABEF are of equal area, then :
View Solution
