Plot the region in the first quadrant in which the points are nearer to the origin thatn to the line . Solution in Tamil
Point P(x,y) lies in the first quadrant. Therefore,
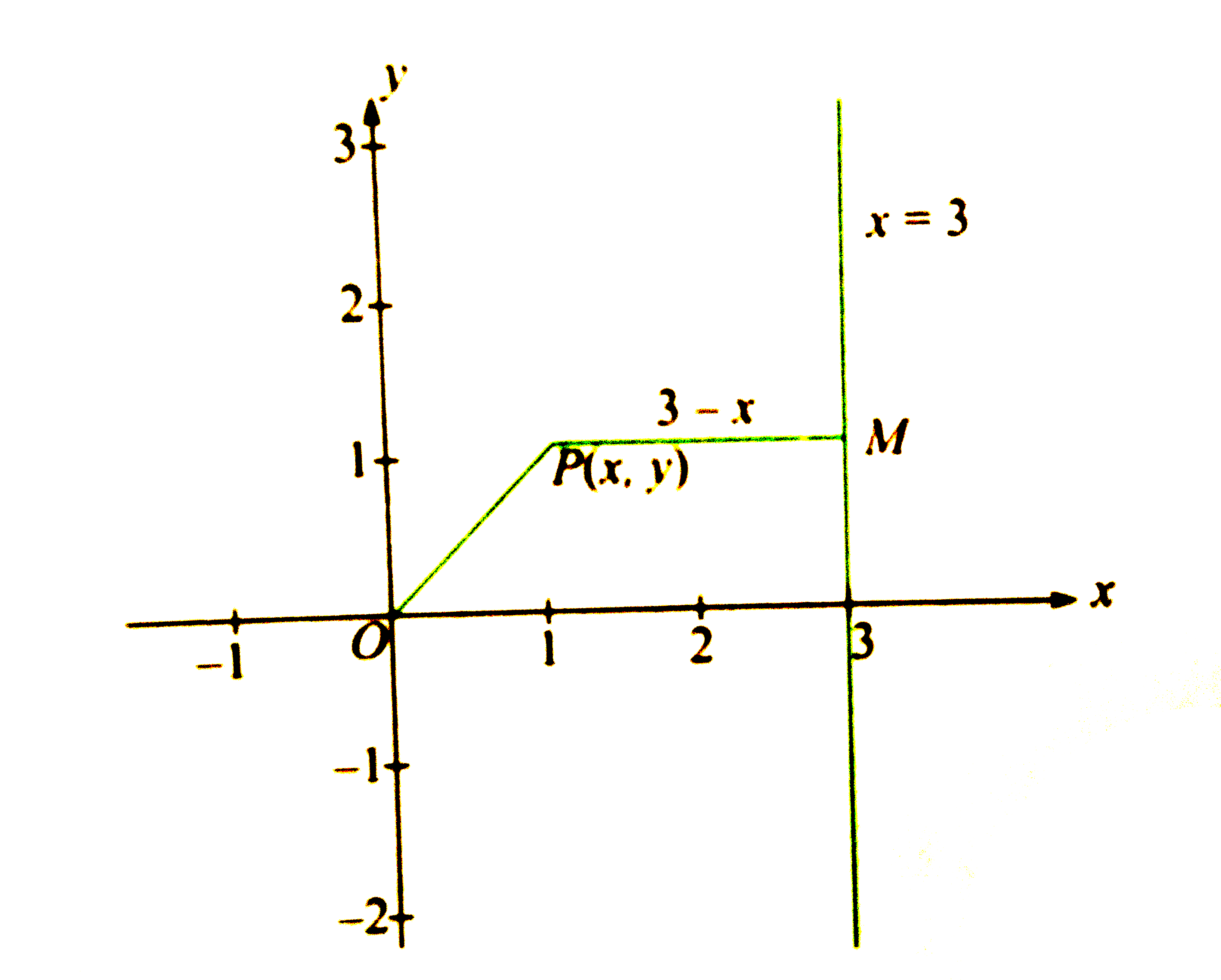
Also point P(x,y) is nearer to the origin than to the line x=3
Distance of P from line x-3=0 is PM =3-x
According to the question,
Points satisfying above inequality lie inside parabola in the first quadrant.
is concave to the left, having axis as
x-axis and vertex at and directrix x=3
The required region as shown in the figure.

sq. units
Topper's Solved these Questions
- AREABOOK - CENGAGECHAPTER - AREAEXERCISE - Exercise 9.1
9 Videos
- AREABOOK - CENGAGECHAPTER - AREAEXERCISE - Exercise 9.2
14 Videos
- APPLICATIONS OF DERIVATIVESBOOK - CENGAGECHAPTER - APPLICATIONS OF DERIVATIVESEXERCISE - Subjective Type
2 Videos
- AREA UNDER CURVESBOOK - CENGAGECHAPTER - AREA UNDER CURVESEXERCISE - Question Bank
10 Videos
Similar Questions
Find the area of the smaller part of the circle x2+y2=a2 cut off by the line x=a√2.
View SolutionFind the area lying in the first quadrant and bounded by the curve y=x3 and the line y=4x.
View SolutionProve that for λ>1, the equation xlogx+x=λ has least one solution in [1,λ].
View SolutionThe area of the region (s) enclosed by the curves y=x2 and y=√|x| is
View SolutionPlot the region in the first quadrant in which points are nearer to the origin than to the line x=3.
View Solutionfind what values of A the point (a,a+1) lies inside the smaller region x^(2)+y^(2)=9 and the line x+y=2 in the first quadrant.
View SolutionArea of the region in the first quadrant exclosed by the X-axis, the line y=x and the circle x2+y2=32 is
View SolutionArea of the region in the first quadrant exclosed by the X-axis, the line y=x and the circle x2+y2=32 is
View Solutionवक्रो y=√x,2y−x+3=0 तथा x अक्ष से घिरे उस क्षेत्र का क्षेत्रफल ज्ञात कीजिए जो प्रथम चतुर्थांश में स्थित है |
View SolutionWhich of the following is an equation of a line that will have points in all the quadrants except the first ?
View SolutionFind the area of the region if the first quadrant bounded by the parabola y2=4x, the line x+y=3 and y-axis.
View SolutionArea of the region in the first quadrant exclosed by the X-axis, the line y=x and the circle x2+y2=32 is
View SolutionPlot the region in the first quadrant in which points are nearer to the origin than to the line x=3.
View SolutionPlot the region in the first quadrant in which points are nearer to the origin than to the line x=3.
View Solutionfind the area of the region in the first quadrant enclosed by the X -axis , the line y=x and the circle x2+y2=32
View SolutionFind the area of the region bounded by the parabola y2=x and the line y=x in the first quadrant.

View Solution
