Plot the region in the first quadrant in which points are nearer to the origin than to the line x=3.Solution in Tamil
Point P(x,y) lies in the first quadrant.
So x,y>0
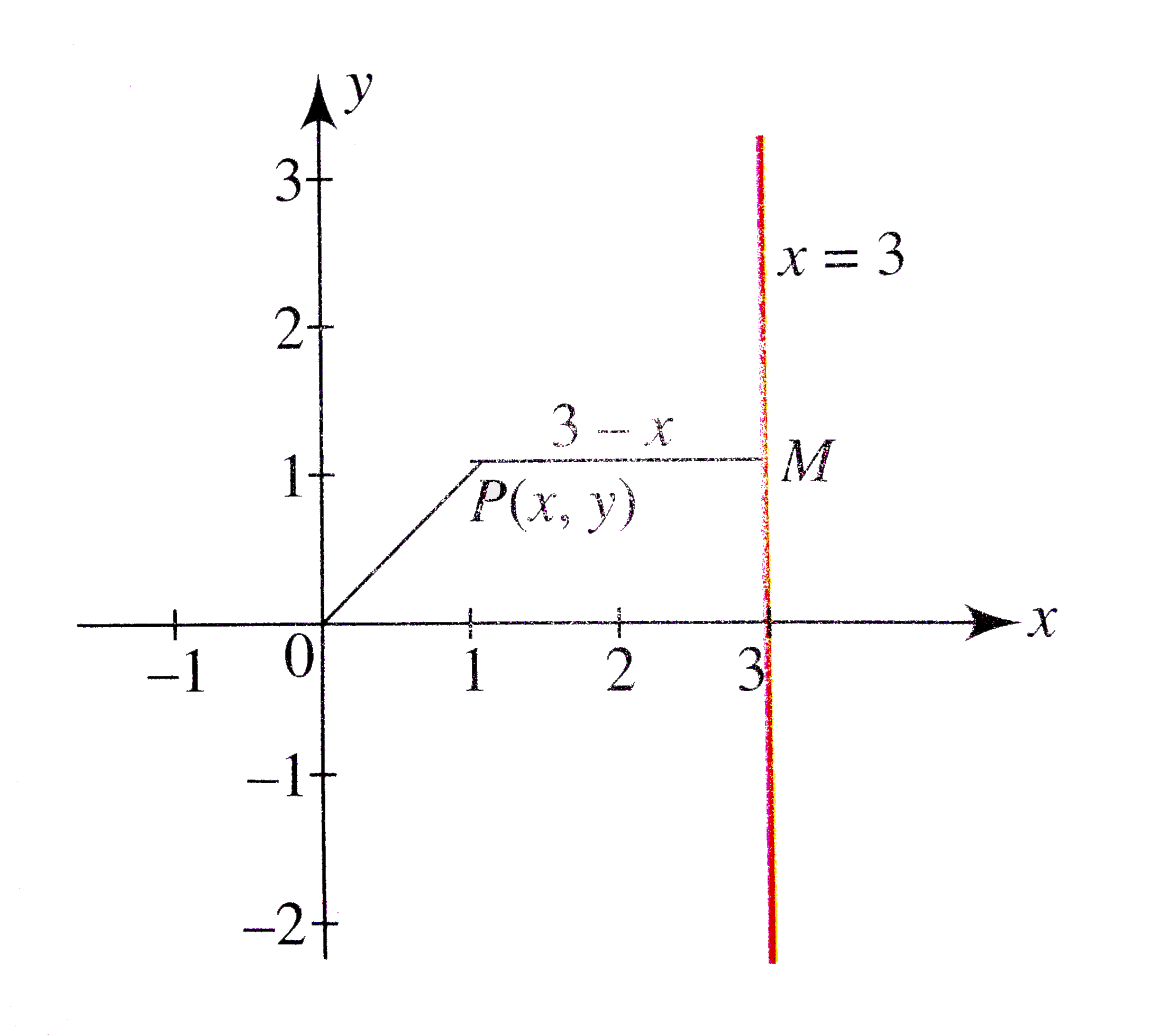
Also point P(x,y) is nearer to the origin than to the line x=3.
Now OP=√x2+y2
Distance of P from the line x−3=0 is PM =3−x.
According to the questions, OP < PM
⇒ √x2+y2<(3−x)
⇒ x2+y2<x2−6x+9
⇒ y2<−6x+9
⇒ y2<−6(x−32)
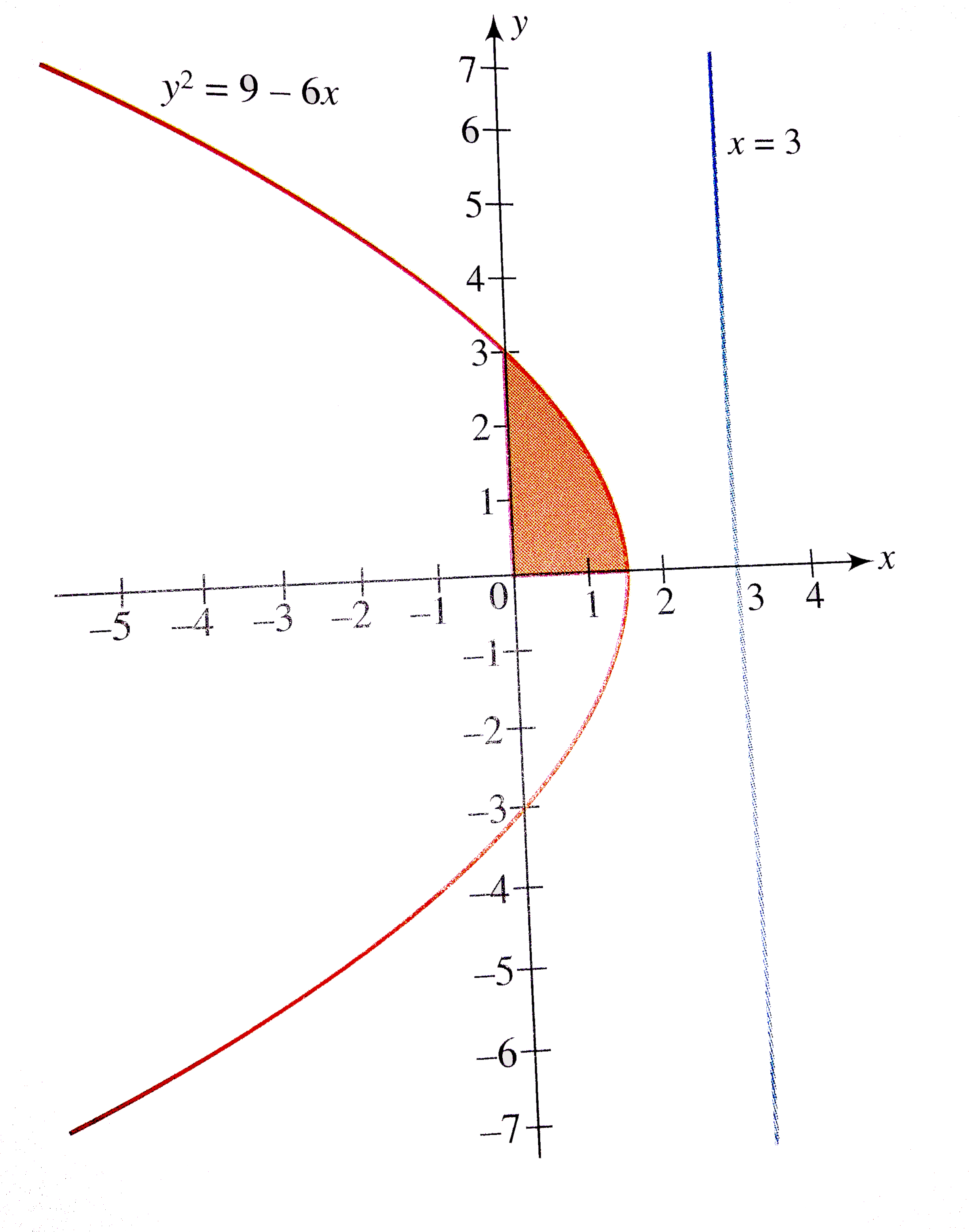
Points satisfying the above inequality lie inside the parabola y2=9−6x in the first quadrant.
Parabola y2=−6(x−32) is concave to the left, having axis as the x-axis, vertex at (32,0) and directrix x=3.
The required region as shown in the following figure.
Topper's Solved these Questions
- BOOK - CENGAGECHAPTER - GRAPHS OF ELEMENTARY FUNCTIONS EXERCISE - Exercise34videos
GRAPHS OF ELEMENTARY FUNCTIONS
- BOOK - CENGAGECHAPTER - GRAPHS OF POLYNOMIAL AND RATIONAL FUNCTIONSEXERCISE - Exercises4videos
GRAPHS OF POLYNOMIAL AND RATIONAL FUNCTIONS
- BOOK - CENGAGECHAPTER - GRAPHS OF TRIGONOMETRIC FUNCTIONSEXERCISE - Exercise22videos
GRAPHS OF TRIGONOMETRIC FUNCTIONS
Similar Questions
Draw the graph of y=1(1/x).
08:33View SolutionSketch the graph of an example of a rational function f that satisfies all the given conditions.
(i) f(0)=0,f(1),limx→∞f(x)=0,f is odd
(ii) limx→0+f(x)=∞,limx→0−f(x)=−∞,limx→∞f(x)=1,limx→−∞f(x)=1
(iii) limx→−2f(x)=∞,limx→−∞f(x)=3,limx→∞f(x)=3,f(0)=006:40View SolutionDraw the graph of y= cosec 2x−cot2x. Is f(x) periodic ? If yes, what is its fundamental period ?
06:11View SolutionPlot the region in the first quadrant in which points are nearer to the origin than to the line x=3.
View SolutionArea of the region in the first quadrant exclosed by the X-axis, the line y=x and the circle x2+y2=32 is
01:40View SolutionArea of the region in the first quadrant exclosed by the X-axis, the line y=x and the circle x2+y2=32 is
06:51View SolutionConsider two regions
R1:points P are nearer to (1,0) than to x=−1.
R2:Points P are nearer to (0,0) than to (8,0) Find the area of the region common to R1andR2.View SolutionThe point (other than origin) for which abscissa is equal to the ordinate will lie in the quadrant
04:57View SolutionFind the area of the region if the first quadrant bounded by the parabola y2=4x, the line x+y=3 and y-axis.
06:54View SolutionThe points (other than origin) for which abscissa is equal to the ordinate will lie in the quadrant
03:21View SolutionArea of the region in the first quadrant exclosed by the X-axis, the line y=x and the circle x2+y2=32 is
03:29View SolutionPlot the region in the first quadrant in which points are nearer to the origin than to the line x=3.
06:03View SolutionPlot the region in the first quadrant in which points are nearer to the origin than to the line x=3.
02:35View SolutionConsider two regions
R1:points P are nearer to (1,0) than to x=−1.
R2:Points P are nearer to (0,0) than to (8,0) Find the area of the region common to R1andR2.06:15View Solutionfind the area of the region in the first quadrant enclosed by the X -axis , the line y=x and the circle x2+y2=32
06:40View Solution

