PM is a median of the ΔPQR. PM is extended to N such that PM = MN. If O be the mid-point of MN and if area of ΔPQR be 40 sq.cm, then the area of the ΔQOM is- Solution in Bengali
20 sq.cm
10 sq.cm
25 sq.cm
30 sq.cm
Step by step video & image solution for PM is a median of the DeltaPQR. PM is extended to N such that PM = MN. If O be the mid-point of MN and if area of DeltaPQR be 40 sq.cm, then the area of the DeltaQOM is- by Maths experts to help you in doubts & scoring excellent marks in Class 9 exams.
Updated on:21/07/2023Topper's Solved these Questions
- THEOREMS ON AREASBOOK - CALCUTTA BOOK HOUSECHAPTER - THEOREMS ON AREASEXERCISE - EXERCISE-3
40 Videos
- SET THEORYBOOK - CALCUTTA BOOK HOUSECHAPTER - SET THEORYEXERCISE - EXERCISE-1
37 Videos
- THEOREMS ON CONCURRENCEBOOK - CALCUTTA BOOK HOUSECHAPTER - THEOREMS ON CONCURRENCEEXERCISE - EXERCISE Long-answer type questions
17 Videos
Similar Questions
D is any point on the side QR of the parallelogram PQRS. ΔPQDandΔSDR have the areas 16 sq.cm and 20 sq.cm respectively, then QD : RD =
View SolutionState which of the following are sets and which are not:
A=A group of students of class-IX having heights from 4ft to 5ft,
View SolutionFind the value of k for which the given value is a solution of the given equation 7x2+kx−3=0 at x=23
View SolutionAD और PM त्रिभुजों ABC और PQR की क्रमशः माध्यिकाएँ हैं , जबकि ΔABC~ΔPQR है । सिद्ध कीजिए कि ABPQ=ADPM है ।
View SolutionAD और PM त्रिभुजों ABC और PQR की क्रमशः माध्यिकाएँ हैं , जबकि ΔABC~ΔPQR है । सिद्ध कीजिए कि ABPQ=ADPM है ।
View SolutionIn ΔPQR, seg PM is median. PM=9, PQ2+PR2=290 then find length of seg QR.
View SolutionIn ΔPQR ,seg PM is a median , PM=9 and PQ∘+PR2=290. Find the length of QR.
View SolutionIf AD and PM be two medians of ΔABC and ΔPQR respectively, where ΔABC~ΔPQR, then prove that ABPQ=ADPM.
View SolutionSeg PM is a median of ΔPQR. If PQ=40,PR=42 and PM =29, find QR.
View Solutionsides AB and BC and median AD of a triangle ABC are respectively proportional to side PQ and QR median PM of ΔPQR (see Fig ). Show that ΔABC~ΔPQR
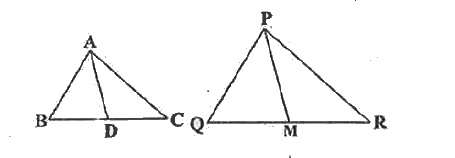
View SolutionIf Adand PM are medians of triangles ABC and PQR, respectively where ΔABC~ΔPQR , prove that ABPQ=ADPM
View SolutionIn ΔPQR, D is the mid-point of ¯¯¯¯¯¯QR.then¯¯¯¯¯¯¯PM is ___________,PD is___________. Is QM=MR?
View SolutionSides AB and BC and median AD of a DeltaABC are respectively proportional to sides PQ and QR and median PM of ΔPQR (see the given figure). Show that ΔABC~ΔPQR.
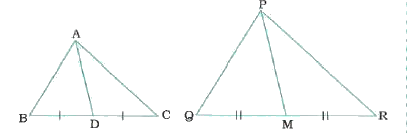
View SolutionSides AB and BC and median AD of a DeltaABC are respectively proportional to sides PQ and QR and median PM of ΔPQR (see the given figure). Show that ΔABC~ΔPQR.

View SolutionIf AD and PM are medians of triangles ABC and PQR respectively , where ΔABC~ΔPQR, prove that ABPQ=ADPM.
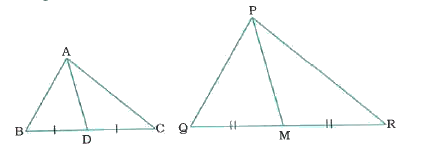
View Solution
