PQ is a tangent to a circle with centre O at the point P. If △OPQ is an isosceles triangle, then ∠OQP is equal to :
30∘
45∘
60∘
90∘
The correct Answer is:B
Topper's Solved these Questions
- CIRCLES BOOK - OSWAL PUBLICATIONCHAPTER - CIRCLES EXERCISE - VERY SHORT ANSWER TYPE QUESTIONS
9 Videos
- CIRCLES BOOK - OSWAL PUBLICATIONCHAPTER - CIRCLES EXERCISE - SHORT ANSWER TYPE QUESTIONS
6 Videos
- CIRCLES BOOK - OSWAL PUBLICATIONCHAPTER - CIRCLES EXERCISE - CASE -BASED MCQs
15 Videos
- C.B.S.E 2020 CLASS -X (OUTSIDE DELHI)BOOK - OSWAL PUBLICATIONCHAPTER - C.B.S.E 2020 CLASS -X (OUTSIDE DELHI)EXERCISE - OUTSIDE DELHI SET -III ( SECTION- D )
2 Videos
- CONSTRUCTIONSBOOK - OSWAL PUBLICATIONCHAPTER - CONSTRUCTIONSEXERCISE - Assertion and Reasoning Based Questions
2 Videos
Similar Questions
Knowledge Check
PQ is a tangent to a circle with centre O at the point P. If ΔOPQ is an isoceless triangle, then ∠OQP is equal to
A30∘B45∘C60∘D90∘The tangent at a point A of a circle with centre O intersects the diameter PQ of the circle (when extended) at the point B. If ∠BAP=125∘, then ∠AQP is equal to :
A45∘B55∘C60∘D50∘
If two tangents are inclined at 60∘ are drawn to a circle of radius 3cm then find length of each tangent.
OR
PQ is a tangent to a circle with centre O at point P. If ΔOPQ is an isosceles triangle, then find ∠OQP.
View SolutionIn figure PQ is tangent to the circle with centre at O at the point B , if ∠AOB=100∘, then ∠ABP is equal to

View SolutionIn figure PQ is tangent to the circle with centre at O at the point B , if ∠AOB=100∘, then ∠ABP is equal to

View SolutionIn figure-3, PQ is tangent to the circle with centre at O, at the point B. if ∠AOB=100∘, then ∠ABP is equal to
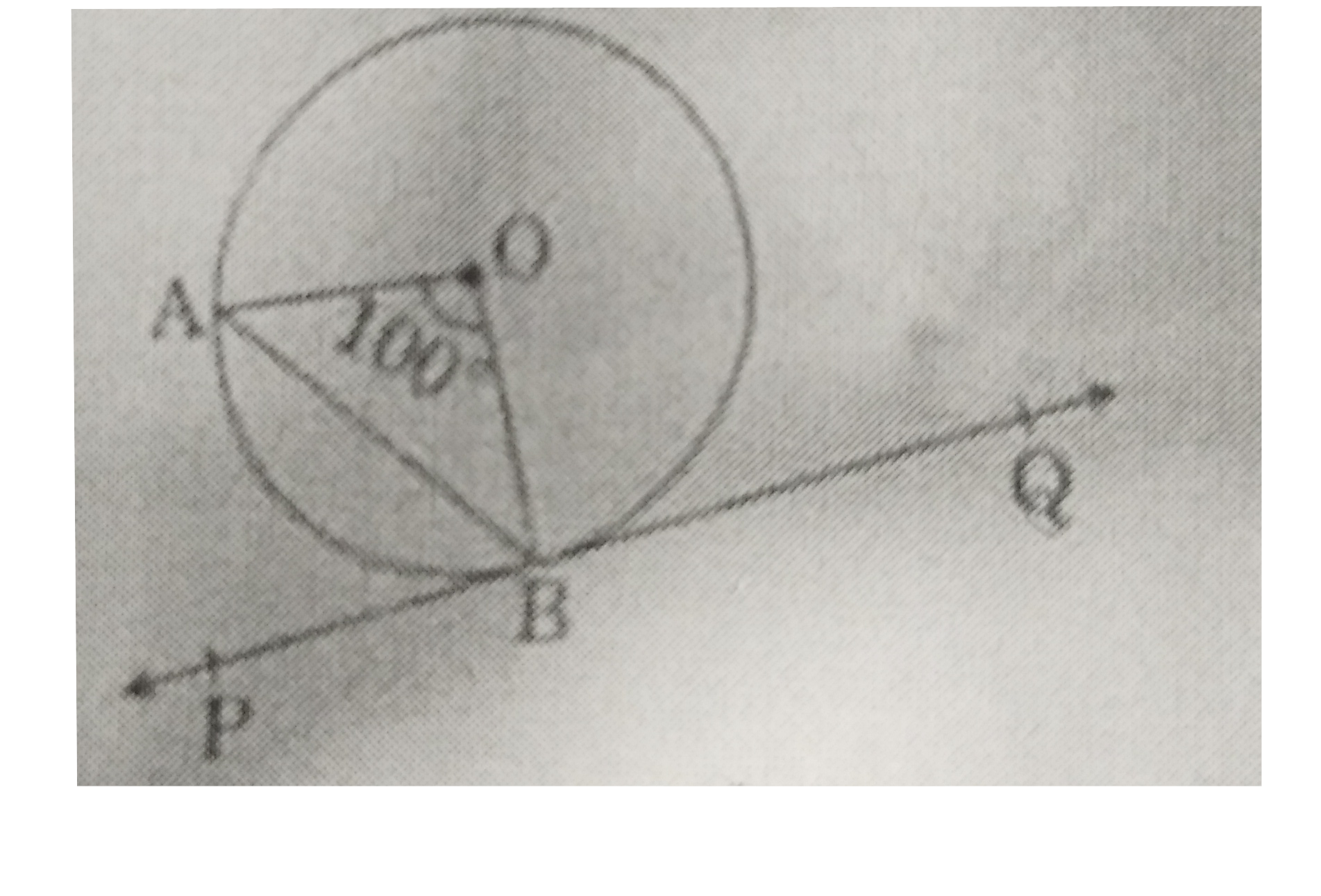
View SolutionIn figure-3, PQ is tangent to the circle with centre at O, at the point B. if ∠AOB=100∘, then ∠ABP is equal to

View SolutionPA and PB are tangents to a circle with centre O from point P. OP is equal to the diameter of the circle. Prove that ABP is equilateral triangle,
View Solution
