PQR is a triangle right angled at P. If PQ=10cmandPR=24cm, find QR
To find the length of side QR in triangle PQR, which is right-angled at P, we can use the Pythagorean theorem. The theorem states that in a right-angled triangle, the square of the length of the hypotenuse (QR in this case) is equal to the sum of the squares of the lengths of the other two sides (PQ and PR).
1. Identify the sides of the triangle:
- PQ = 10 cm (one leg)
- PR = 24 cm (the other leg)
- QR = ? (the hypotenuse)
2. Apply the Pythagorean theorem:
The Pythagorean theorem is given by the formula:
QR2=PQ2+PR2
3. Substitute the known values into the equation:
QR2=(10cm)2+(24cm)2
4. Calculate the squares:
QR2=100cm2+576cm2
5. Add the squares:
QR2=676cm2
6. Take the square root to find QR:
QR=√676cm2
QR=26cm
Final Answer:
The length of QR is 26 cm.
- PQ = 10 cm (one leg)
- PR = 24 cm (the other leg)
- QR = ? (the hypotenuse)
The Pythagorean theorem is given by the formula:
QR2=PQ2+PR2
QR2=(10cm)2+(24cm)2
QR2=100cm2+576cm2
QR2=676cm2
QR=√676cm2
QR=26cm
The length of QR is 26 cm.
Topper's Solved these Questions
- THE TRIANGLE AND ITS PROPERTIESBOOK - NCERTCHAPTER - THE TRIANGLE AND ITS PROPERTIESEXERCISE - EXERCISE 6.1
1 Videos
- THE TRIANGLE AND ITS PROPERTIESBOOK - NCERTCHAPTER - THE TRIANGLE AND ITS PROPERTIESEXERCISE - EXERCISE 6.2
2 Videos
- THE TRIANGLE AND ITS PROPERTIESBOOK - NCERTCHAPTER - THE TRIANGLE AND ITS PROPERTIESEXERCISE - EXERCISE 6.4
6 Videos
- SYMMETRYBOOK - NCERTCHAPTER - SYMMETRYEXERCISE - EXERCISE 14.1
9 Videos
Similar Questions
Knowledge Check
ΔPQR is right angled at point Q. If PQ=8cmand PR=(QR+2)cm. What is the value (in cm) of PR?
A17B15C19D18ΔPQR is right angled at point Q. If PQ=8cmand PR=(QR+2)cm. What is the value (in cm) of PR?
A17B15C19D18In a triangle PQR, PX bisects QR. PX is the angle bisector of angle P. If PQ=12 cm and QX=3 cm, then what is the area (in cm2) of triangle PQR?
A12√3B8√15C18√2D9√15
ΔPQRis right-angled at PSperpQRIf PQ=5cmand PR=12cm, find the area of ΔPQR.Also find the length of PS
View SolutionTriangle PQR is a right-angled at Q. If PQ=6 cm , PR=10 cm, then QR is equal to:
त्रिभुज PQR एक समकोण त्रिभुज है जिसमें Q समकोण है | यदि PQ = 6 सेमी, PR = 10 सेमी है, तो QR किसके बराबर होगा ?
View SolutionPQR is a right angled triangle at Q with QR =12 a=cm and PQ=5cm. A circle with centre O is inscribed in △PQR. Find the radius of the circle.
View SolutionIn a triangle PQR, right angled at Q. PQ=5 cm, QR=12 cm. Find the length of QM , if M is the mid point of PR .
View SolutionIn the figure below, PQR is a right-angled triangle, right angled at P. A perpendicular line PS is drawn from P to QR. PR = 5 cm and PQ = 12 cm.
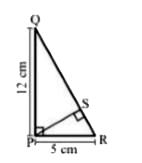
What is RS:SQ?
View Solution