PQRS is a parallelogram , if ∠PQS=40∘andPS=QS , then ∠SQR−∠QRS = ___________.
60∘
20∘
30∘
45∘
The correct Answer is:A
To solve the problem, we need to find the value of ∠SQR−∠QRS in the parallelogram PQRS, given that ∠PQS=40∘ and PS=QS.
1. Identify the Properties of the Parallelogram:
- In a parallelogram, opposite sides are equal and opposite angles are equal.
- Given that PS=QS, we can conclude that triangle PQS is isosceles.
2. Determine Angles in Triangle PQS:
- Since PS=QS, the angles opposite these sides are equal. Thus, ∠PQS=∠PSQ.
- Given ∠PQS=40∘, we can denote ∠PSQ=40∘.
3. Calculate the Remaining Angle in Triangle PQS:
- The sum of angles in a triangle is 180∘.
- Therefore, we can find ∠QPS:
∠QPS=180∘−∠PQS−∠PSQ=180∘−40∘−40∘=100∘.
4. Identify Angles in the Parallelogram:
- Since PQRS is a parallelogram, opposite angles are equal. Thus, ∠QRS=∠PQR=40∘ and ∠SQR=∠QPS=100∘.
5. Calculate ∠SQR−∠QRS:
- Now we can find the difference:
∠SQR−∠QRS=100∘−40∘=60∘.
Final Answer:
∠SQR−∠QRS=60∘.
- In a parallelogram, opposite sides are equal and opposite angles are equal.
- Given that PS=QS, we can conclude that triangle PQS is isosceles.
- Since PS=QS, the angles opposite these sides are equal. Thus, ∠PQS=∠PSQ.
- Given ∠PQS=40∘, we can denote ∠PSQ=40∘.
- The sum of angles in a triangle is 180∘.
- Therefore, we can find ∠QPS:
∠QPS=180∘−∠PQS−∠PSQ=180∘−40∘−40∘=100∘.
- Since PQRS is a parallelogram, opposite angles are equal. Thus, ∠QRS=∠PQR=40∘ and ∠SQR=∠QPS=100∘.
- Now we can find the difference:
∠SQR−∠QRS=100∘−40∘=60∘.
∠SQR−∠QRS=60∘.
Topper's Solved these Questions
- MOCK TEST PAPERBOOK - PEARSON IIT JEE FOUNDATIONCHAPTER - MOCK TEST PAPEREXERCISE - Questions
5 Videos
- MENSURATIONBOOK - PEARSON IIT JEE FOUNDATIONCHAPTER - MENSURATIONEXERCISE - Concept Application (Level 3 )
8 Videos
- PERCENTAGESBOOK - PEARSON IIT JEE FOUNDATIONCHAPTER - PERCENTAGESEXERCISE - Concept Application (LEVEL 3)
7 Videos
Similar Questions
Knowledge Check
PQRS is a rhombus in which ∠R = 60°. Then PR : QS =
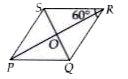 A√3 : 1B√3:√2C3 : 1D3 : 1
A√3 : 1B√3:√2C3 : 1D3 : 1In Δ PQR,PS is the bisector of ∠PandPT⊥QR, where ∠ Q = 60 and ∠R = 30 then ∠TPS is equal to
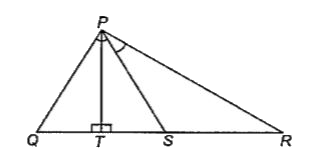 A10B30C60D15
A10B30C60D15PQRS is a parallelogram in which PR is perpendicular to QS. If PR=8cm and QS=6 cm, then find PS
A5cmB4cmC7cmD6cm
PQRS is rhombus with ∠QPS=50∘. Find ∠PQS.
View SolutionIn the adjoining figure if PQRS is a parallelogram where ∠PQR=100and∠SPR=40. Find ∠PRQand∠SRQ.
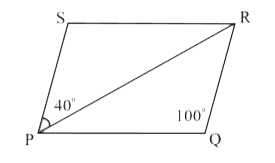
View SolutionIn parallelogram PQRS,angle PQR=125∘ and ∠PRS=25∘, Find the value of ∠SPR.
View Solution□ PQRS is a rhombus and ∠PQS=42∘ , then find ∠ PQR. Justify .
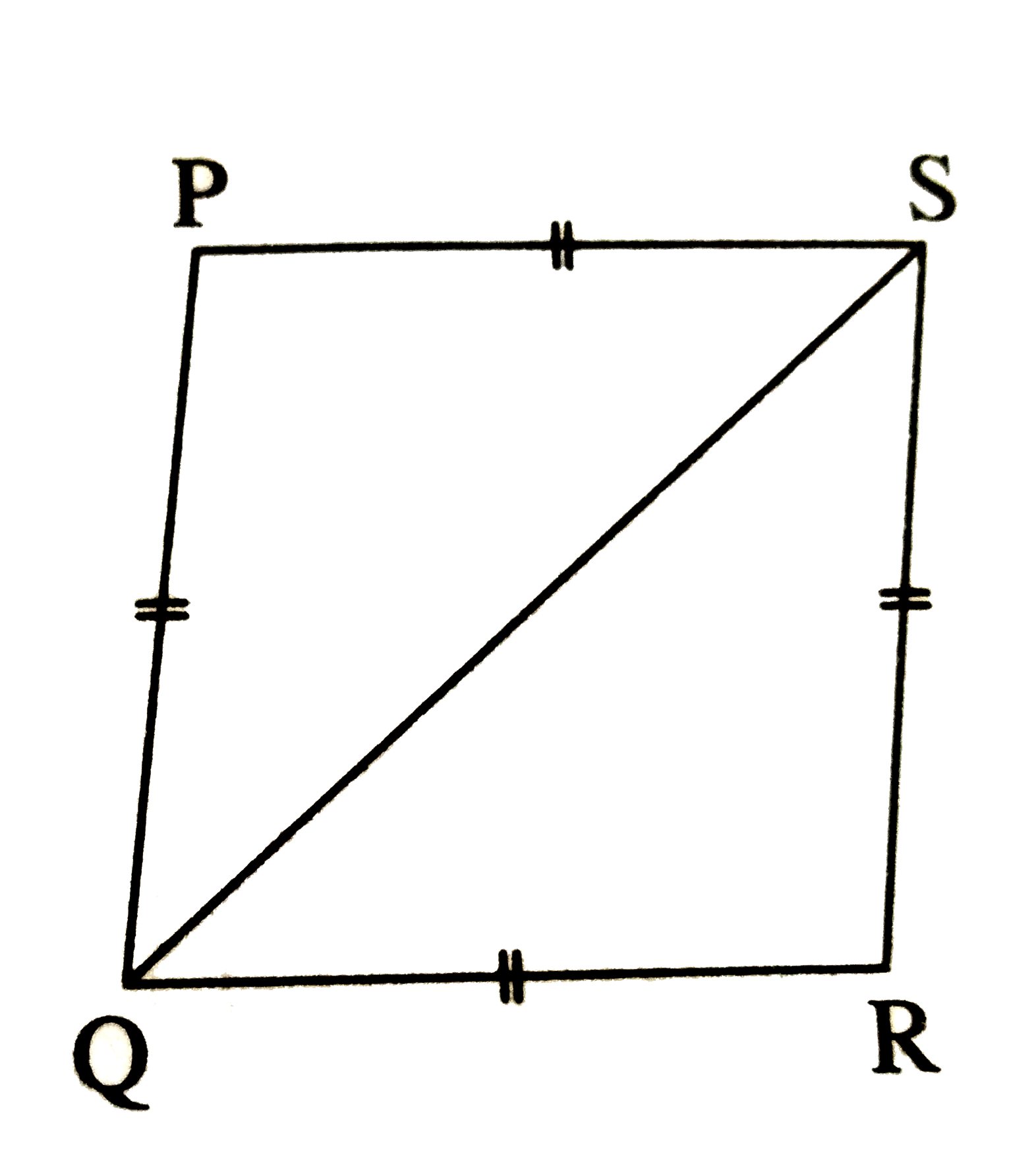
View SolutionPQRS is a parallelogram in which PR is perpendicular to QS. If PR=8cm and QS=6 cm, then find PS
View Solution
