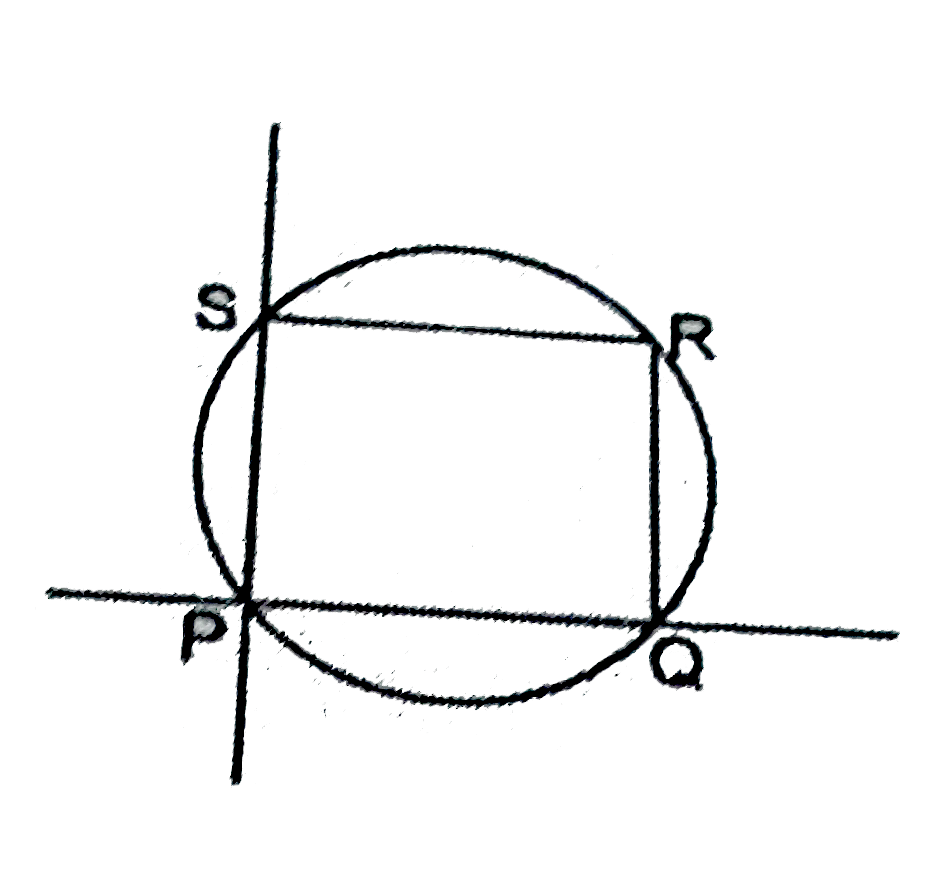
PQRS is a square of side 'b'. Prove that the equation of circumcircle of square PQRS, where PQ and PS are the axes, is $x^{2} + y^{2} = b (x + y)$ .

Video Solution

Text Solution

Verified by Experts

Draw a square of side 'b' taking PS as the axes. Now the co-ordinates of its vertices are $P (0, 0), Q (b, 0), R (b, b) and S (0, b)$
From the equation of circumcircle of square PQRS,
$(x_{1}, y_{1}) = (0, 0) and (x_{2}, y_{2}) = (b, b)$
Equation of circle
$(x - x_{1}) (x - x_{2}) + (y - y_{1}) (y - y_{2}) = 0$
$\Rightarrow (x - 0) (x + b) + (y - 0) (y - b) = 0$
$\Rightarrow x^{2} - b x + y^{2} - b y = 0$
$\Rightarrow x^{2} + y^{2} = b (x + y)$ .

Updated on:21/07/2023

Equation of circumcircle of square OACB of side a, where
OA and OB are along coordinate axes , is
A $x^{2} + y^{2} - a x + a y = 0$
B $x^{2} + y^{2} + a x - a y = 0$
C $x^{2} + y^{2} + a x + a y = 0$
D $x^{2} + y^{2} - a x - a y = 0$
The sides of a square are $x = 4, x = 7, y = 1$ and $y = 4$ . The equation of the circumcircle of the square is $:$
A $x^{2} + y^{2} + 11 x = 4 y + 17 = 0$
B $x^{2} + y^{2} + 7 x - 6 y + 18 = 0$
C $x^{2} + y^{2} - 11 x - 3 y + 30 = 0$
D $x^{2} + y^{2} - 11 x - 5 y + 32 = 0$
Solve for x and y.
$x + y = a + b$
$a x - b y = a^{2} - b^{2}$
A $x = b, y = - b$
B $x = b, y = a$
C $x = - a, y = - b$
D $x = a, y = b$