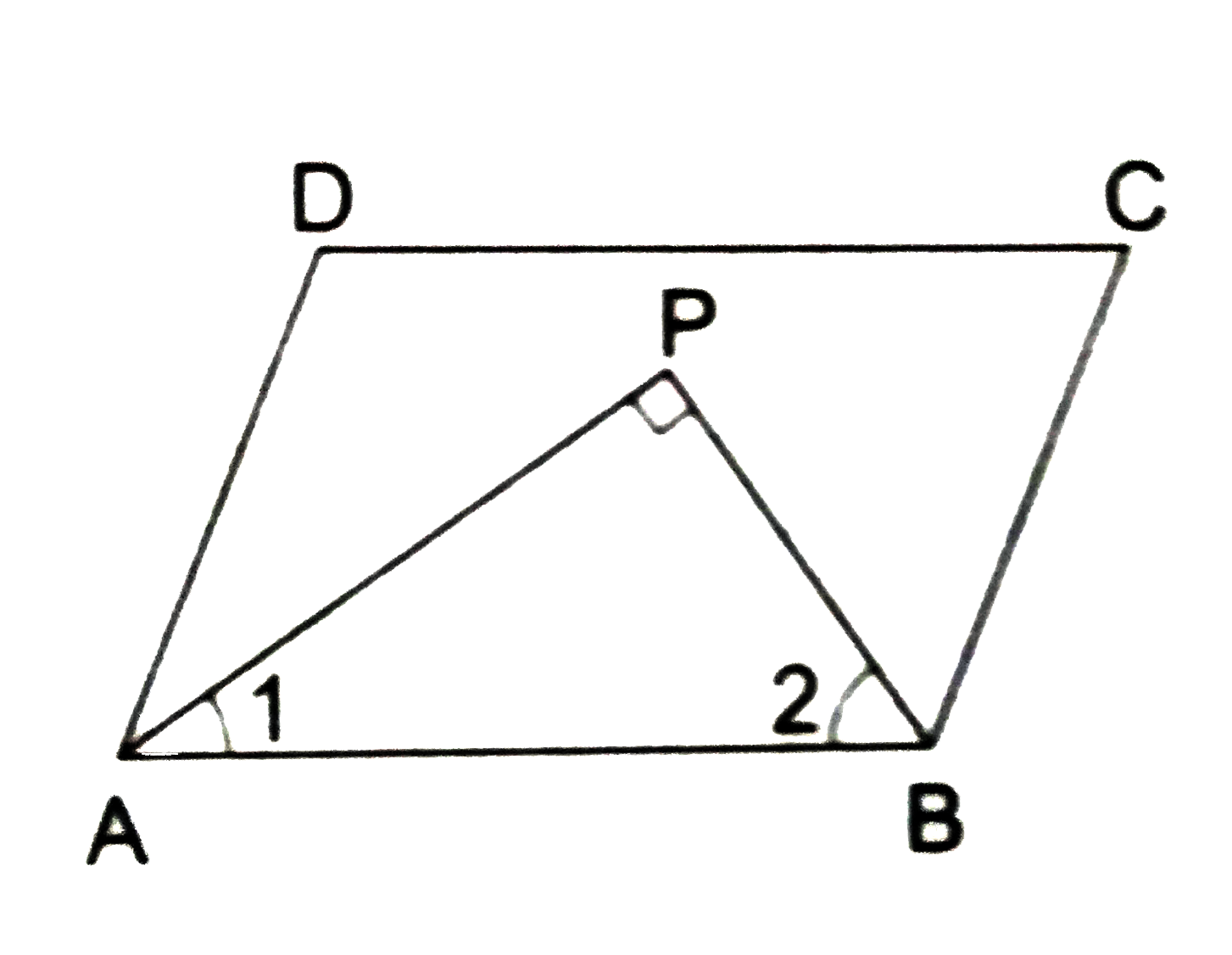
Prove that in a parallelogram, the bisectors of any two consecutive angles intersect at right angles.
Video Solution
Text Solution
GIVEN A ||gm ABCD in which the bisectors of two consecutive angles intersect at a point P.
TO PROVE
PROOF AD ||BC and AB is a transversal
.
In we have
|
Updated on:21/07/2023
Topper's Solved these Questions
- BOOK - RS AGGARWALCHAPTER - QUADRILATERALSEXERCISE - Exercise 10 A10videos
QUADRILATERALS
- BOOK - RS AGGARWALCHAPTER - QUADRILATERALSEXERCISE - EXERCISE 10B27videos
QUADRILATERALS
- BOOK - RS AGGARWALCHAPTER - QUADRILATERALSEXERCISE - Matching of Columns:2videos
QUADRILATERALS
- BOOK - RS AGGARWALCHAPTER - PROBABILITYEXERCISE - Multiple Choice Questions (Mcq)16videos
PROBABILITY
- BOOK - RS AGGARWALCHAPTER - TRIANGLESEXERCISE - MULTIPLE-CHOICE QUESTIONS (MCQ)10videos
TRIANGLES
Similar Questions
Knowledge Check
- Question 1 - Select One
In a parallelogram ABCD, the sum of any two consecutive angles is 180degree and opposite angles are equal.
In the given figure, find ∠A in the parallelogram .
 A90∘B60∘C30∘D110∘
A90∘B60∘C30∘D110∘ - Question 2 - Select One
In a parallelogram ABCD, the sum of any two consecutive angles is 180∘ and opposite angles are equal.
In a parallelogram ABCD,∠D=115∘ , determine the measure of ∠Aand∠BA∠A=85∘,∠B=115∘B∠A=65∘,∠B=65∘C∠A=65∘,∠B=115∘D∠A=75∘,∠B=105∘ - Question 3 - Select One
In a parallelogram ABCD, the sum of any two consecutive angles is 180∘ and opposite angles are equal.
Find the value of ∠Qand∠P , if ∠P=10aand∠R=50∘ in a parallelogram PQRS.A∠=50∘,∠P=130∘B∠Q=130∘,∠P=50∘C∠Q=100∘,∠P=120∘D∠Q=50∘+∠P=100∘
In a parallelogram ABCD , prove that sum of any two consecutive angles is 180∘
View SolutionIn the parallelogram ABCD, the internal bisectors of the consecutive angles B and C intersect at P. Use vector method to find ∠BPC
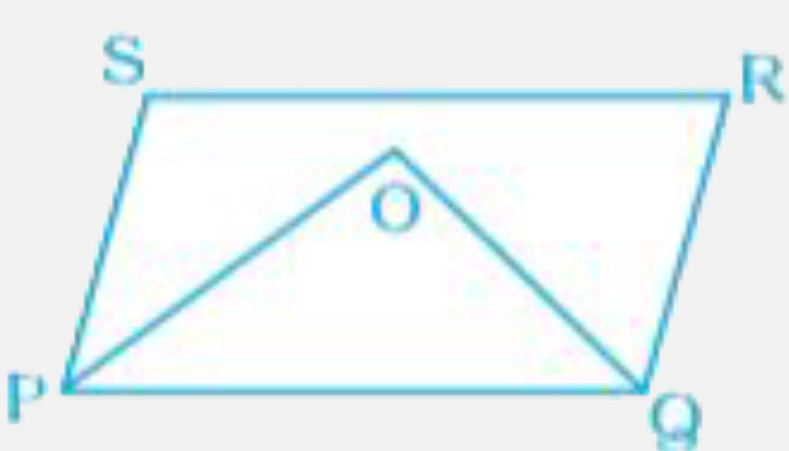
View SolutionIn a parallelogram PQRS, the bisectors of ∠P and ∠Q meet at O. Find ∠POQ.
 View Solution
View SolutionIn a parallelogram ABCD, bisectors of consecutive angles A and B intersect at P. Find the measure of ∠APB :
View SolutionIn a parallelogram ABCD, the bisectors of ∠Aand∠B intersect each other at point P. Prove that ∠APB=90∘.
View Solution

