Prove that the equation 2sinx=|x|+a has no solution for a∈(3√3−π3,∞).
Video Solution
Text Solution
sinx=12|x|+a2
Draw the graphs of y=2sinxandy=|x|.
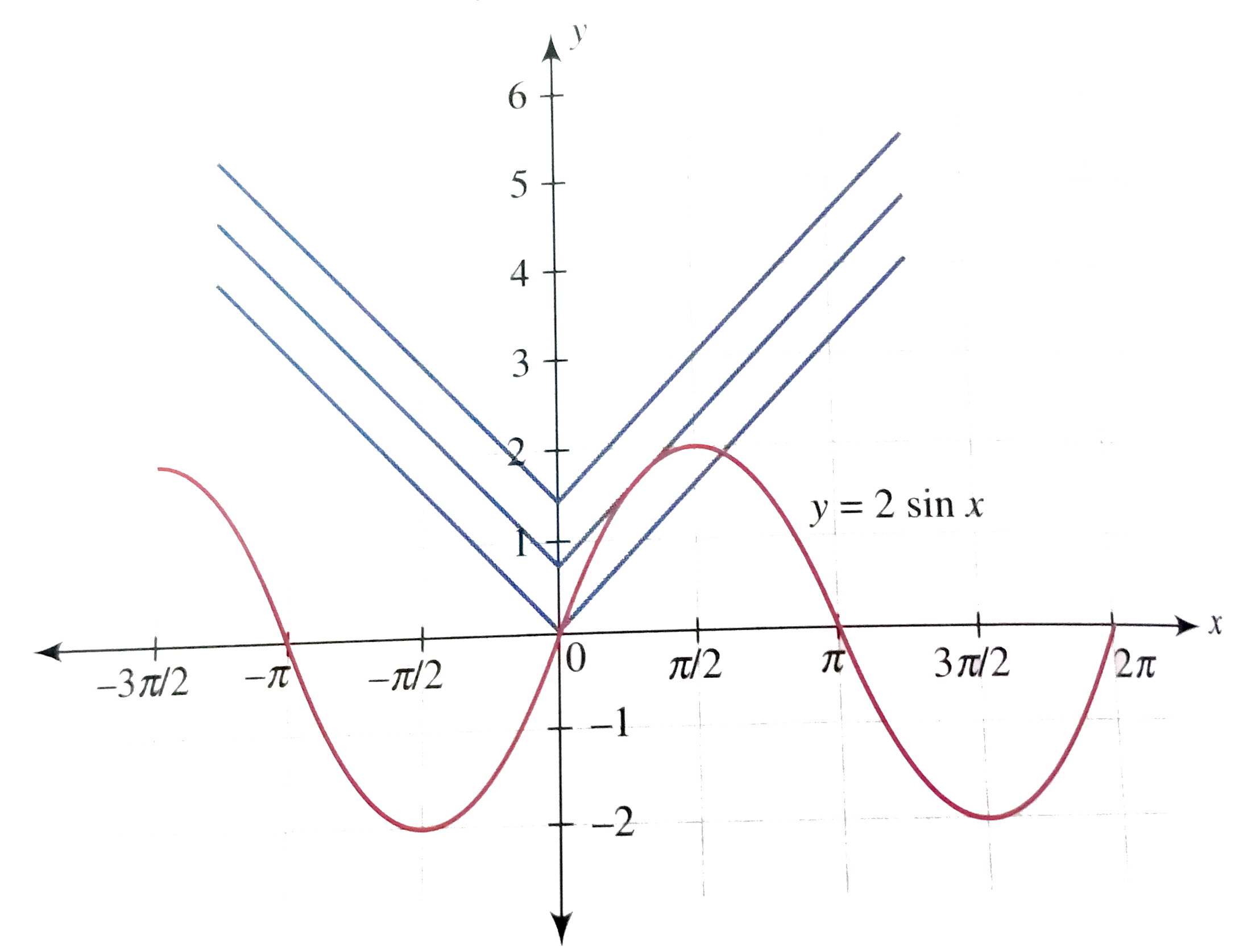
The equation 2sinx=|x|+a will have a solution so long as the line y=|x|+a intersects or at least touches the curve y=2sinx. When the graphs touch, we have
dydx=2cosx=1,⇒x=π3
Hence for no solution,
π3+a>2sinπ3
⇒a>3√3−π3
|
Updated on:21/07/2023
Topper's Solved these Questions
Similar Questions
Prot that the equation kcosx−3sinx=k+1 possess a solution if k∈(−∞,4].
View SolutionThe equation |sinx|=sinx+3has in[0,2π]
View SolutionSolve the equation √3cosx+sinx=√2.
View SolutionSolve the equation √3cosx+sinx=√2.
View SolutionSolve the equation √3cosx+sinx=1 for −2π<x≤2π.
View SolutionFind number of solution of the equation 2sinx+5sin2x+8sin3x+...∞=1 for x∈[0,2π].
View SolutionFind the solution of the equation (sinx+cosx)sin2x=a(sin3x+cos3x) located between π2 and π and for which values of 'a' does this equation have at most one solution satisfying the condition π2≤x≤π.
View SolutionNumber of solutions of the equation 2sin3x+6sin2x−sinx−3=0 in (0,2π), are
View SolutionThe solutions of the system of equations sinxsiny=√34,cosxcosy=√34 are
View SolutionFor x∈(0,π) the equation sinx+2sin2x−sin3x=3 has
View Solution

