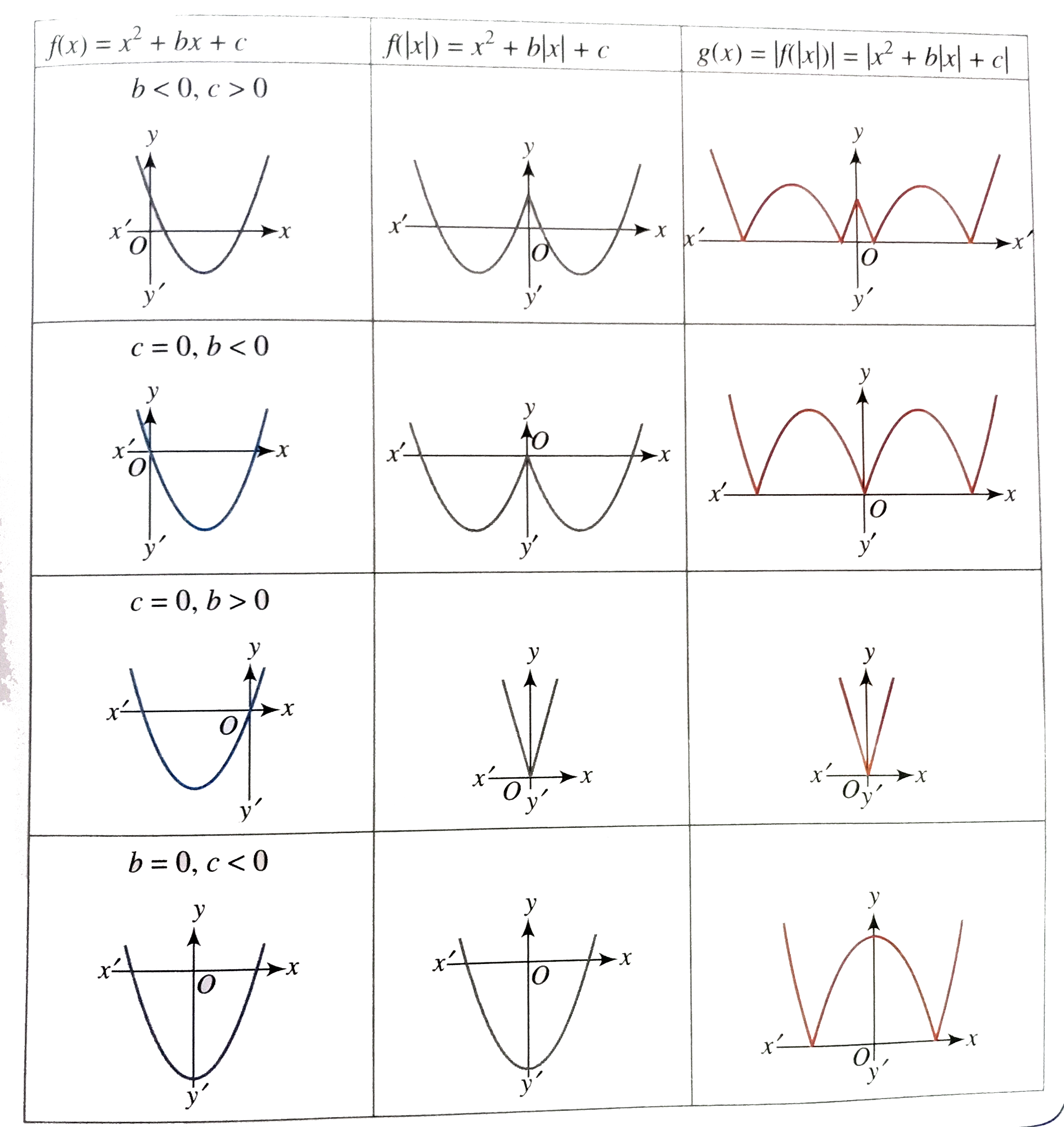
Consider the function f(x)=x2+bx+c, where D=b2−4c>0, then match the follwoing columns.

Topper's Solved these Questions
Similar Questions
Consider that f(x)=ax2+bx+c,D=b2−4ac , then which of the following is not true ?
View SolutionConsider the function f(x)=(ax+1bx+2)x, where a,b>0, the limx→∞f(x) is
View SolutionConsider the function f(x)=min{∣∣x2−4∣∣,∣∣x2−1∣∣}, then the number of points where f(x) is non - differentiable is/are
View SolutionConsider the function f(x)={2x≤02x>0 Find limx→2
View Solutionconsider the function f:R→R,f(x)=x2−6x+4x2+2x+4
f(x) is
View SolutionConsider the function f(x)=|x−2|+|x−5|,c∈R.
Statement 1: f'(4)=0
Statement 2: f is continuous in [2,5], differentiable in (2,5),
View SolutionLet f:[0,5]→[0,5) be an invertible function defined by f(x)=ax2+bx+C, where a,b,c∈R,abc≠0, then one of the root of the equation cx2+bx+a=0 is:
View SolutionLet f:[0,5]→[0,5) be an invertible function defined by f(x)=ax2+bx+C, where a,b,c∈R,abc≠0, then one of the root of the equation cx2+bx+a=0 is:
View SolutionConsider the function f(x)={xsinπx,forx>00,forx=0 The, the number of point in (0,1) where the derivative f′(x) vanishes is 0 (b) 1 (c) 2 (d) infinite
View SolutionIf the range of the function f(x)=3x2+bx+c is [0,∞) then value of b23c is
View Solution