Prove that the sum of the squares of the diagonals of parallelogram is equal to the sum of the squares of its sides.

Video Solution

Text Solution

Verified by Experts

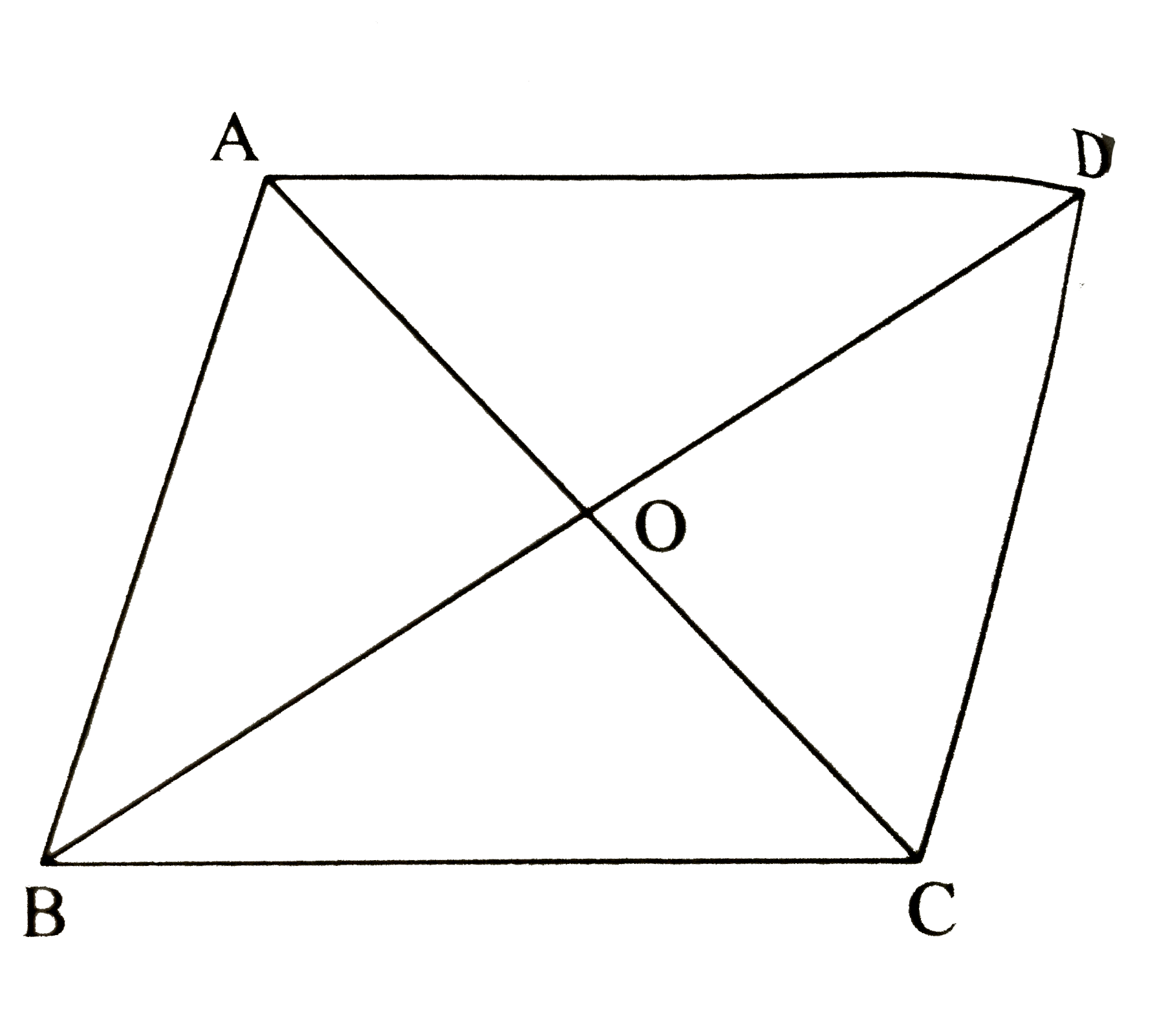
Given : $() □ A B C D$ is a parallelogram
$(i i)$ Diagonals $A C$ and $B D$ intersect at $O$ .
To prove: $A C^{2} + B D^{2} = A B^{2} + B C^{2} + C D^{2} + A D^{2}$
Proof : $□ A B C D$ is a parallelogram……..(Given)
$\begin{matrix} ∴ C D = A B ... ... (1) A D = B C ... ... ... . (2) \end{matrix}}$ (Opposide sides of parallelogram are equal )
Also $A O = O C = \frac{1}{2} A C$ ...... $(3)$
$B O = O D = \frac{1}{2} B D$ ........ $(4)$ .........(Diagonals of parallelogram bisect each other)
In $Δ A B C$ ,
seg $B O$ is the median ......(By definition)
$∴$ by Apollonius theorem,
$A B^{2} + B C^{2} = 2 B O^{2} + 2 O C^{2}$
$∴ A B^{2} + B C^{2} = 2 {(\frac{1}{2} B D)}^{2} + 2 {(\frac{1}{2} A C)}^{2}$ ........[From $(3)$ and $(4)$ ]
$∴ A B^{2} + B C^{2} = 2 \times \frac{1}{4} B D^{2} + 2 \times \frac{1}{4} A C^{2}$
$∴ A B^{2} + B C^{2} = \frac{1}{2} B D^{2} + \frac{1}{2} A C^{2}$
Multiplying each term by $2$ , we get,
$2 A B^{2} + 2 B C^{2} = B D^{2} + A C^{2}$
$∴ A B^{2} + A B^{2} + B C^{2} + B C^{2} = B D^{2} + A C^{2}$
$∴ A B^{2} + C D^{2} + B C^{2} + A D^{2} = B D^{2} + A C^{2}$ ......[From $(1)$ and $(2)$ ]
$∴ A B^{2} + B C^{2} + C D^{2} + A D^{2} = B D^{2} + A C^{2}$
i.e. $A C^{2} + B D^{2} = A B^{2} + B C^{2} + C D^{2} + A D^{2}$ .

|

Updated on:21/07/2023

Class 10 MATHS TRIANGLES

Topper's Solved these Questions

Similar Questions

NAVNEET PUBLICATION - MAHARASHTRA BOARD-PYTHAGORAS THEOREM-3.5 (4 mark each)

Home
Ask Doubt
Profile