$□ A B C D$ is a parallelogram. The diagonals $A C$ and $B D$ intersect at point $M$ . The length of seg $A C$ , $A B$ and $A D$ is $24$ , $22$ and $34$ respectively. Find the length of seg $B D$ .

Video Solution

Text Solution

Verified by Experts

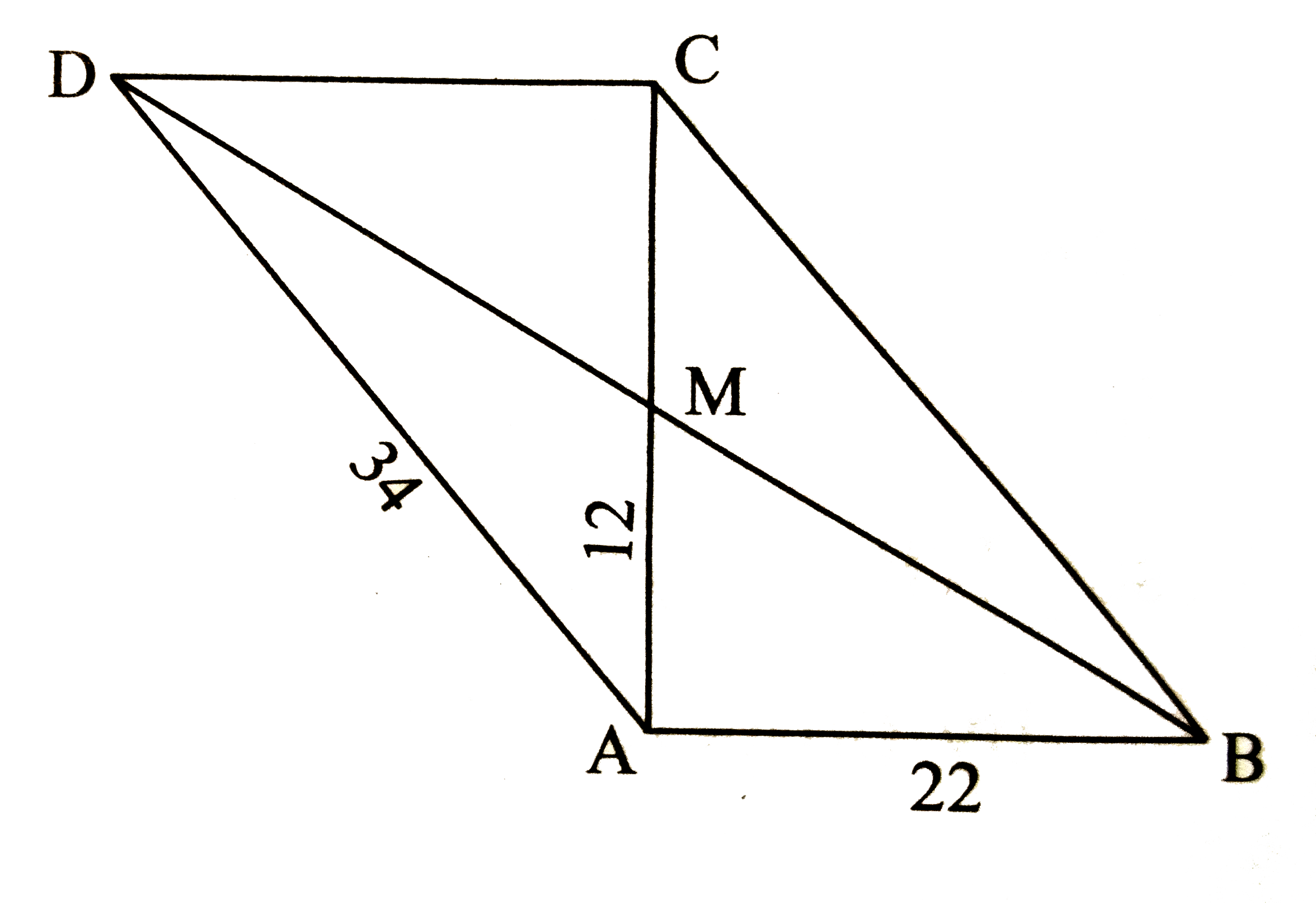
$□ A B C D$ is a parallelogram
The diagonals of parallelogram bisect each other
$∴ A M = \frac{1}{2} A C = \frac{1}{2} \times 24 = 12$
$M$ is the midpoint of diagonal $B D$
$∴$ seg $A M$ is the median of $Δ A B D$
$∴$ by Apollonius theorem,
$A B^{2} + A D^{2} = 2 A M^{2} + 2 B M^{2}$
$∴ {(22)}^{2} + {(34)}^{2} = 2 {(12)}^{2} + 2 B M^{2}$
$∴ 484 + 1156 = 2 (144) + 2 B M^{2}$
$∴ 1640 - 288 = 2 B M^{2}$
$∴ 2 B M^{2} = 1352$
$∴ B M^{2} = \frac{1352}{2}$
$∴ B M^{2} = 676$
$∴ B M = 26$
$B M = \frac{1}{2} B D$ .........(Diagonals of paralelogram bisect each other)
$∴ 26 = \frac{1}{2} \times B D$
$∴ B D = 52$

Updated on:21/07/2023

If ABCD is a parallelogram, then $- - \to A C - - - \to B D =$
A $4 - - \to A B$
B $3 - - \to A B$
C $2 - - \to A B$
D $- - \to A B$
ABCD is a parallelogram in which diagonals AC and BD intereset at O. If E, F, G and H are the mid points of AO, DO, CO and BO respectively, then the ratio of the perimeter of the quadrilateral EFGH to the perimeter of parallelogram ABCD is:
A0.042361111111111
B0.043055555555556
C0.04375
D0.044444444444444
In a quadrilateral ABCD, with unequal sides if the diagonals AC and BD intersect at right angles, then
A $A B^{2} + B C^{2} = C D^{2} + D A^{2}$
B $A B^{2} + C D^{2} = B C^{2} + D A^{2}$
C $A B^{2} + A D^{2} = B C^{2} + C D^{2}$
D $A B^{2} + B C^{2} = 2 (C D^{2} + D A^{2})$