Prove that two different circles cannot intersect each other at more than two points.
Step by step video & image solution for Prove that two different circles cannot intersect each other at more than two points. by Maths experts to help you in doubts & scoring excellent marks in Class 9 exams.
Updated on:21/07/2023Topper's Solved these Questions
Similar Questions
Can two isothermal curves intersect each other?
View SolutionWhy don't two magnetic field lines intersect each other?
View SolutionTwo streamlines cannot cross each other. Why?
View SolutionTwo equal chord AB and CD of a circle with centre O, intersect each other at point P inside the circle.
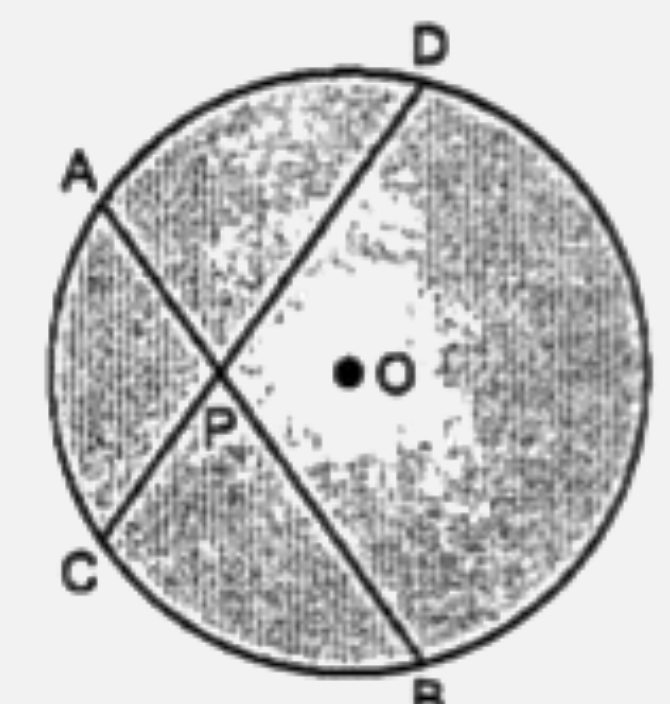
Prove that:
BP=DP
View SolutionTwo circles with centres A and B intersect each other at points P and Q. Prove that the centre-line AB bisects the common chord PQ perpendicularly.
View SolutionIn the figure, two equal chords AB and CD of a circle with centre O, intersect each other at E, Prove that AD=CB
View SolutionIn triangle LMN, bisector of interior angles at L and N intersect each other at point A. Prove that :
AM bisects angle LMN.
View SolutionIn parallelogram ABCD, the bisectors of adjacent angles A and D intersect each other at point P. prove that ∠APD=90∘.
View SolutionIf two diameters of a circle intersect each other at right angles, then quadrilateral formed by joining their end points is a
View SolutionConsider the circles x2+(y−1)2=9,(x−1)2+y2=25. They are such that these circles touch each other one of these circles lies entirely inside the other each of these circles lies outside the other they intersect at two points.
View Solution
