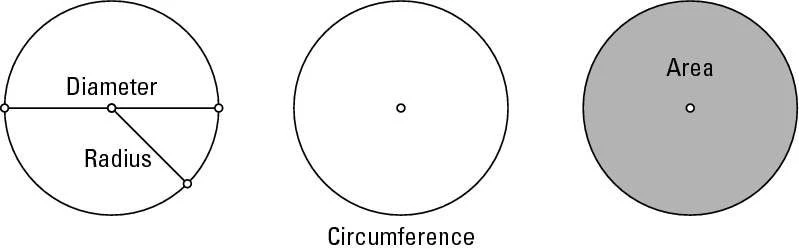
Radius; Perimeter and Area
What is a Circle?
A circle closed plane geometric shape. In specialized terms, a circle is a location of a point surrounding and moving at a fixed distance away from the stationary point. It may be considered as anything which is round. The distance of a peripheral point from the centre point is the radius of the circle. Let us look at some properties and terms associated with the circle.
Radius of Circle
It is the line which connects the centre point of the circle and the circumference of the circle. It is typically represented by 'r' or 'R'. The radius value is used in determining the area and perimeter of the circle. We will look at some solved examples in the end.
Diameter of Circle
It is the line whose both ends touches the circumference of the circle and passes through the centre point of the circle. It is twice the measure of the radius. It is typically represented by 'd' or 'D'.
If we know the length of the diameter of the circle, we can find the radius of the circle, such as;
r = d/2 or R = D/2
Old mathematicians figured out that the perimeter of a circle is always somewhat more than three times the radius of a circle. Since at that point, they limited that "little multiple times" to a worth called pi (pronounced "pie"), designated by the Greek letter π.
The decimal estimation of π isn't precise — it goes on for all eternity, however, most of the time, individuals allude to it as being roughly 3.14 or 22/7, whichever form works best in specific computations. The estimation of pi is roughly 3.1415926535897… The value of π is a non-ending decimal number.
Circumference of Circle
The perimeter is the distance around a circle or any curved geometrical shape. It is the one-dimensional straight diameter of the limit across any two-dimensional round surface. It follows the same rule behind finding the edge of any polygon, which is the reason ascertaining the outline of a circle which is also known as the border of a circle.
A circle is characterized as a shape with all the points are equidistant from a point at the inside.
Formula for Circumference of a Circle
The Circumference (or) perimeter of a circle = 2πr
where,
r is the radius of the circle
π is the numerical constant with a rough (up to two decimal points) estimation of 3.14
Once more,
Pi (π) is a special numerical constant, it is the proportion of circuit to the diameter of any circle.
For instance: If the radius of the circle is 8 cm, then determine its
Given: Radius, r = 8cm
Circumference of circle = 2πr
= 2 x 3.14 x 8
= 50.24 cm
What is Area of Circle?
Any geometrical shape has its own area. This area is the region covered by the shape in a two-dimensional plane. The area of the circle is the space covered by the circumference of circle in a two-dimensional plane. To find the area of a circle we use the formula, A= πr2, where r is the radius of the circle.
This formula is used to measure the region covered by a round field or a plot. Suppose, in the event that you have the plot to fence it, at that point the area formula will assist you with checking how much fencing is required. Or on the other hand suppose in the event that you need to purchase cloth material ofr round table, at that point how much segment of fabric is expected to cover it totally.
Formula for Area of Circle
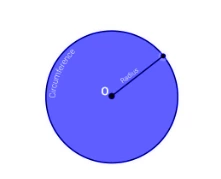
From the above picture, we can see a circle, where radius r from the middle 'o' to the circumference of the circle. At that point, the area for this circle, A, is equivalent to the product of pi and square of the radius.
A = πr2 square units
Here, the estimation of pi, π = 22/7 or 3.14
Related Videos:
- What is Circle?
- Arc of a Circle
- Length of an Arc
- Chord of a circle
- Circular Disc and Concentric circles
- Diameter
Solved Examples on Area and Perimeter of Circle
Example 1: Find the radius of the circle, whose area is 66 cm2?
Solution:
Area of circle= 66 cm2
We know, area of the circle, A = π x r2
Substituting the value:
66 = π x r2
66 = 22/7 x r2
r2 = 66 x 7/22
r2 = 21
r = 4.58 cm
Example 2: Calculate the area and the perimeter of the circle if the radius is 14 cm.
Solution:
Given: Radius, r = 14 cm
Area of the circle is πr2 sq. units
Putting the value of ‘r’ in the formula
A = (22/7) × 14 × 14
A = 22 × 2 x 14
A= 22 x 28
A = 616 cm2
Now, the formula for the circumference of the circle is 2πr units
Putting the value of ‘r’ in the above formula
C = 2 × (22/7)× 14
C = 4×22
C = 88 cm
Thus, the perimeter of the circle is 88 cm
Example 3: If the radius of a circle is 18 cm, calculate its area.
Solution: Radius of circle, r, = 18 cm
The area of the circle, A, = πr2
A = 3.14 x 18 x 18
A = 1017.36 cm 2
Example 4: Find the area of the circle having diameter of 14 cm.
Solution:
Given, diameter, D, = 14 cm
So, radius will be = 14/2 = 7 cm
Area of a circle, A, = πr2
A = 22/7 x 7 x 7
A= 22 x 7
Area of circle= 154 cm2
Example 5: find rge area of the circle having the circumference of 42 cm.
Solution:
Given, circumference of the circle, C= 42 cm
Formula of circumference, C =2πr
Putting the value of C,
2πr = 42
or r = 42/2π = 21/π
Now we will substitute the value of ‘r’ in the formula of area of the circle.
Area of the circle = πr2
A = π(21/π)2
On simplifying we get,
Are of circle = 21 x 21x7/22
A= 140.31 cm2
Important Chapters:


Similar Questions
Knowledge Check
- Question 1 - Select One
Find the perimeter and area of the shaded portion of the adjoining diagram:
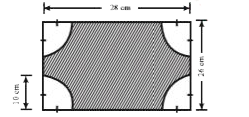 A90.8cm,414cm2B181.6cm,423.7cm2C90.8cm,827.4cm2D181.6cm,827.4cm2
A90.8cm,414cm2B181.6cm,423.7cm2C90.8cm,827.4cm2D181.6cm,827.4cm2 - Question 2 - Select One
If P is the perimeter and r is the radius of a sector, then the area of the sector is maximum, if
AP=rBP=2rCP=3rDP=4r
Areas Related To Circles - Perimeter|Perimeter Of Circle (Circumference)|Area|Area Of Circle|Perimeter And Area Semi Of Circle|Perimeter And Area Of A Ring|Questions|OMR
View SolutionPerimeter and Area of a circle
View SolutionA rectangle and a square are of equal area. If the length and the perimeter of a rectangle are 25 cm and 58 cm respectively, then find the perimeter and area of the square?
View SolutionIf the perimeter and the area of a circle are numerically equal, then the radius of the circle is.
View SolutionArea and Perimeter of rectangle
View SolutionArea and perimeter of a rectangle
View Solution

