What is Circle ?
Circle
You are familiar with different types of geometric shapes and figures. Well, out of those, the circle is a fascinating kind that is present around us in various objects. Some day to day life examples of circles is the moon, sun, or any circular objects including a bottle cap. So, we will try to get the right understanding of the circle definition as well as the area circle formula that are all associated with geometry.
Area of circle
The region which is occupied by the circle in a 2-dimensional plane is called the area of a circle. The area of a circle is defined by the formula A = 2 πr2 So, with the help of this, we can calculate the area of various circular-shaped objects or items.
The radius of the circle is represented by the letter, ‘r.’ Thus it becomes quite easier to get the space measured with the help of the area formula. For example, in order to know the amount of grassing required to be done for your circular lawn, we will use the area formula for circle. This would prove to be quite easy to get the right calculation without any problem at all. In Maths, the concept of the area and perimeter has been introduced to solve different problems. You should keep in mind that a circle does not have a volume due to the reason that it is a two-dimensional shape. So, in this case, you can find only the area and perimeter.
Formula for Area of Circle
Below is a circle that has a radius, ‘r’ which is drawn from the centre ‘o’ to the boundary of the circle. The area for this circle A is equal to the product of pi and square of the radius. You need to understand that the area of a circle, A = πr2 units. Here the value of π = 3.14 or 22/7.
Derivation of Area of Circle Formula
The area of the circle can be both proved and visualized with the help of two methods which are areas of rectangles and area of triangles which have been explained below:
With the use of Areas of Rectangles
Look at the below figures. You would find that there are 16 equal sectors depicted in two different colours in the circle. In this case, the cut-out sectors that have formed the parallelogram-shaped figure will prove to be equal to the area of the circle. Since there are equal areas in the sectors, there will be an equal arc length for each sector.
In this case, the colour red will contribute half of the circumference, while the colour blue will contribute the other half. A noteworthy thing is that if there is an increase in the number of sectors cut, then the parallelogram would take the form of a rectangle where both the breadth and length will be equal to r and πr respectively.
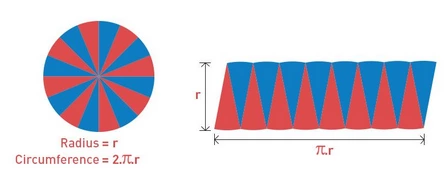
So, in this case, the area of a rectangle (A) would be the same as that of the area of a circle, which is:
A = πr×r
A = πr2
With the use of Areas of Triangles
By making use of Areas of Triangle, you can prove the area of a circle in the right way.
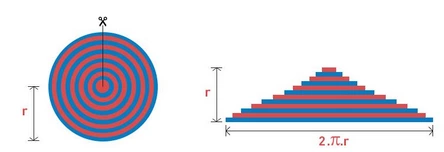
In the above figure, you can find a circle with radius. ‘r’ that has concentric circles. In this case, the result that you would get is a triangle. There will be the equal height of the triangle with the radius of the circle. Moreover, there will be an equal base of the triangle with the circumference of the circle.
As mentioned that the area of the triangle (A) will be equal to the area of the circle, so we have:
A = ½ × base ×height
A = ½ × (2πr) × r
A = πr2
Related Videos:
- Radius, Perimeter and Area
- Arc of a Circle
- Length of an Arc
- Chord of a circle
- Circular Disc and Concentric circles
- Diameter
What is the Surface Area of Circle Formula?
If there is a requirement to measure the area of a circle, then it means the surface area of the circle. In order to find out the surface area of the given length of the diameter or radius, the surface formula can be used. So, here the surface area of the circle = A = π x r2
What is the Circumference of Circle?
The perimeter of closed figures is defined by the length of the boundary. But when it comes to circle, the term, ‘perimeter’ gets changed. So, this is termed as the circumference of the circle. So, this is the length of the boundary of the circle. The length of the straight line which you get by opening the circle is the circumference.

Have a look at the circle above that has got centre ‘o’ and radius ‘r.’ There is also a rope on the right-hand side. Here, the perimeter of the circle is the same as that of the length of the boundary. In order to measure it, we need to use the formula:
Circumference/Perimeter = 2 πr units (here, r is the radius of the circle and π is the pie)
So, here, if we consider the circle with circumference ‘C’ and radius ‘r’, then we get
- π = Diameter/Circumference
- π =C/2r
- C = 2πr
We will now work on some examples to get a good understanding of the application of the different formulas. By doing so, you would be able to get a clear idea on circle and perimeter.
Solved Examples
Question 1:
If the area of a square is equal to the area of the circle. The surface area of a square is 628.318 sq cm. Determine the radius of the circle?
Solution:
By the formula of the surface area of the circle, we know;
A = π x r2
Now, substituting the value:
628.318 = π x r2
628.318 = 3.14 x r2
r2 = 628.318 /3.14
r2 = 200.05
r = √200.05
r = 20 cm
Therefore, the radius of the square is 20 cm
Question 2
Calculate the area of the circle, if the circumference of a circle is 60 cm?
Solution:
Given, the circumference of a circle = 60 cm
We will now apply the formula of circumference, i.e. C =2 πr
So, we can write,
2πr = 60
or r = 60/2π = 30/π
We have now found the value of r. So, now we can find the area;
A = πr2
A = π (30/ π)2
On solving we get,
A = 143.3 sq.cm.
So, the area of the circumference is 143.3 sq cm.
Important Chapters:




Similar Questions
Knowledge Check
- Question 1 - Select One
What is the ratio of the area of circle A to that of circle B ?
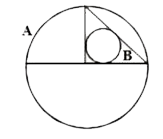 A12B14C2(√2+1)2D2(√2−1)2
A12B14C2(√2+1)2D2(√2−1)2 - Question 2 - Select One
A chord of length 24 cm is at a distance of 5 cm from the centre of a circle. What is its area?
A120cm2B480.67cm2C531.14cm2D389.28cm2 - Question 3 - Select One
The area of circle is seven times the numerical value of its circumference. What is the circumference of the circle?
A616B132C88DCannot be determined
A resistance of 10Ω is bent in the from of a closes circle. What is the effective resistance between the two at the ends of any diameter of this circle ?
View SolutionWhat is the use of a dip circle?
View SolutionAuxiliary circle and eccentric angle
View SolutionEscribed Circle
View SolutionWhat is the number of circles in the following figure?
 View Solution
View Solution

