Ratio of circumference and radius of a circle is equal to
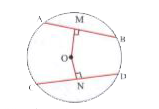
If AB = CD and O is the centre of circle then which of the following can be the values of OM and ON (in cm), respectively?
5, 6
6, 5
4, 4
3, 2
The correct Answer is:A
Topper's Solved these Questions
- CIRCLESBOOK - CENGAGECHAPTER - CIRCLESEXERCISE - OLYMPIAD AND NTSE LEVEL EXERCISES
6 Videos
- CIRCLESBOOK - CENGAGECHAPTER - CIRCLESEXERCISE - TEST YOURSELF (LEVEL 3)
8 Videos
- ALGEBRAIC EXPRESSIONS AND POLYNOMIALS BOOK - CENGAGECHAPTER - ALGEBRAIC EXPRESSIONS AND POLYNOMIALS EXERCISE - OLYMPIAD AND NTSE LEVEL EXERCISES
10 Videos
- LAWS OF EXPONENTS AND LOGARITHMS BOOK - CENGAGECHAPTER - LAWS OF EXPONENTS AND LOGARITHMS EXERCISE - OLYMPIAD AND NTSE LEVEL EXERCISES
10 Videos
Similar Questions
In the adjoining figure, O is the centre of the circle. If the chord AB is equal to the radius of the circle, then find the value of ∠ADB.

View SolutionIn the adjoining figure, O is the centre of the circle. If the chord AB is equal to the radius of the circle, then find the value of ∠ADB.

View Solution
Knowledge Check
The circumference of a circle is equal to the sum of the circumferences of two circles having diameters 36 cm and 20 cm. The radius of the new circle is
A16cmB28cmC42cmD56cmThe third proportional to 9 and 12 is ?
AA) 14BB) 16CC) 18DD) 20
AB and CD are chords of a circle with centre O. AB = 48 cm and its distance from centre O is 10 cm. If the distance of CD from centre O is 24 cm, find the length of CD.
View SolutionO is the centre of the smaller circle, O' is the centre of bigger circle.CD is tangent to the smaller circle,Find the radius of the smaller circle.
View SolutionM and N are the mid-points of two equal chords AB and CD respectively of a circle with centre O. Prove that :
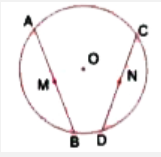
∠AMN=∠CNM.
View SolutionMake a line segment AB of length 8 cm. Taking A as centre and radius 5 cm, draw a circle. With B as centre and radius 6 cm, draw another circle. Mark the two points at which the two circles intersect as C and D. Join CD. Find the angle between AB and CD with the help of a protractor.
View SolutionThe distances of two chords AB and CD from the centre of a circle are 6 cm and 8 cm respectively. Then, which chord is longer?
View SolutionThe distances of two chords AB and CD from the centre of a circle are 6 cm and 8 cm respectively. Then, which chord is longer?
View Solution
