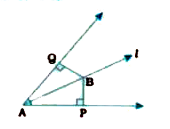
Ray 1 is the bisector of an angle ∠ A and B is any point on I. BP and BQ are perpendiculars from B to the arms of ∠ A (see the given figure). Show that:
(i) △APB=△AQB
(ii) BP = BQ or B is equidistant from the arms of ∠A
 Solution in Gujrati
Solution in Gujrati
The correct Answer is:∠A
Step by step video, text & image solution for Ray 1 is the bisector of an angle angle A and B is any point on I. BP and BQ are perpendiculars from B to the arms of angle A (see the given figure). Show that: (i) triangleAPB=triangleAQB (ii) BP = BQ or B is equidistant from the arms of angleA by Maths experts to help you in doubts & scoring excellent marks in Class 9 exams.
Updated on:21/07/2023Topper's Solved these Questions
Similar Questions
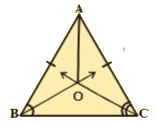
In an isosceles triangle ABC, with AB = AC, the bisectors of ∠Band∠C intersect each other at O. Join A to O. Show that :
(i) OB = OC (ii) AO bisects ∠A
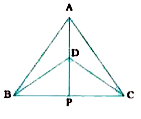
View Solution△ ABC and △ DBC are two isosceles triangles on the same base BC and vertices A and D are on the same side of BC (see the given figure). If AD is extended to intersect BC at P, show that, ( i ) △ABD=△ACD(ii)△ABP=△ACP (iii) AP bisects ∠ A as well as ∠ D. (iv) AP is the perpendicular bisector of BC
View SolutionThe total surface area of a cuboid with length 20 cm, breadth 15 cm and height 10 cm is ……… cm2.
View Solutionline l is the bisector of an angle ∠A and∠Bis any point on l. BP and BQ are perpendiculars from B to the arms of ∠A. Show that:
(i) ΔAPB≅ΔAQB
(ii) BP = BQ or B is equidistant from the arms of ∠A

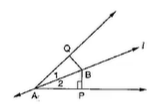
View SolutionIn Figure, line l is the bisector of angle A and B is any point on l.BP and BQ are perpendiculars from B to the arms of A. Show that: APB ≅AQB BP=BQ or B is equidistant from the arms of ∠A
View SolutionDetermine the point of symmetry of a regular hexagon.
View SolutionIn the following figure, AB and BC are equidistant from the centre 'O' of the Show that
(a) ABC is an isosceles triangle.
(b) OB bisects angle ABC.
ltimg src="https://d10lpgp6xz60nq.cloudfront.net/physics_images/PS_MATH_X_C13_E02_006_Q01.png" width="80%"gt
View SolutionMatch the following Column A to Column B

View SolutionIn the given figure, PQRS is a parallelogram. A and B are the mid-point of ¯¯¯¯¯¯PQ and ¯¯¯¯¯SR respectively. If PS=BR, then the quadrilateral ADBC is a…………………… ,
ltimg src="https://d10lpgp6xz60nq.cloudfront.net/physics_images/PS_MATH_IX_C12_E05_020_Q01.png" width="80%"gt
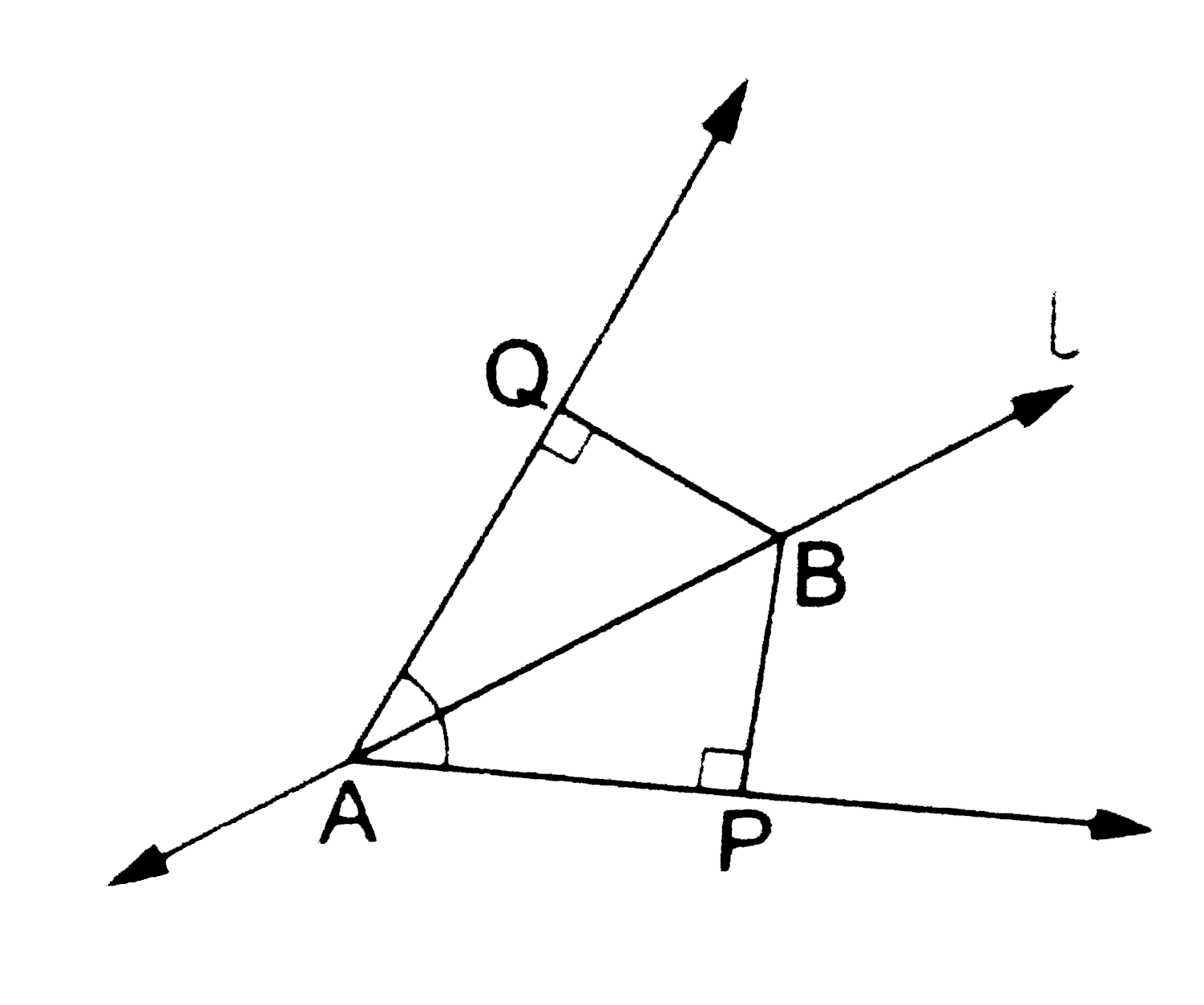
View SolutionIn the given figure, line l is the bisector of an angle ∠A and B is any point on l. If BP and BQ are perpendiculars from B to the arms of ∠A, show that
(i) ΔAPB≅ΔAQB
(ii) BP = BQ, i.e., B is equidistant from the arms of ∠A.
View Solutionरेखा l कोण A को समद्विभाजित करती है और B रेखा l पर स्थित कोई बिंदु है। BP और BQ कोण A की भुजाओं पर B से डाले गए लम्ब हैं। दर्शाइए कि
(i) ΔAPB≅ΔAQB
(ii) BP=BQ है, अर्थात बिंदु B कोण की भुजाओं से समदूरस्थ है।

View Solutionरेखा l कोण A की समद्विभाजक है तथा l पर कोई बिंदु B है| BP और BQ बिंदु B से ∠Aकी भुजाओं पर लम्ब है तो दिखाइये कि-

(i) ΔAPB≅ΔAQB
(ii) BP=BQ
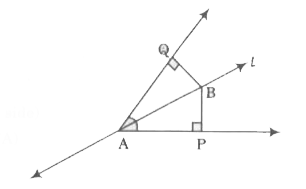
View SolutionLine l is the bisector of an angle ∠A and B is any point on li. BP and BQ are perpendicular forms B to the arms of ∠A. Show that:
△APB≅△AQB
(ii) BP = BQ or B is equidisitant from the arms of ∠A.
View Solutionरेखा l कोण A को सम्द्धिभाजित करती है और B रेखा I पर स्थित कोई बिंदु है | BP और BQ कोण A की भुजाओ पर B से डाले गए लम्ब है ( देखिये आकृति ) | दर्शाइए कि-
(i) ΔPB ~-=ΔAQB
(ii) BP -= BQ है, अर्थात बिन्दु B कोण की भुजाओ से समदूरस्थ है |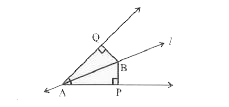
View SolutionIn Figure, line l is the bisector of angle A and B is any point on l.BP and BQ are perpendiculars from B to the arms of A. Show that: APB ≅AQB BP=BQ or B is equidistant from the arms of ∠A
View Solution
