Reduce the equation 3x−2y+4=0 to intercepts form and find the length of the segment intercept the axes.
We have
3x−2y+4=0⇒3x−2y=−4
⇒3x−4+y2=1[on dividing both sides by−4]
⇒x(−43)+y2=1
⇒xa+yb=1,wherea=−43andb=1
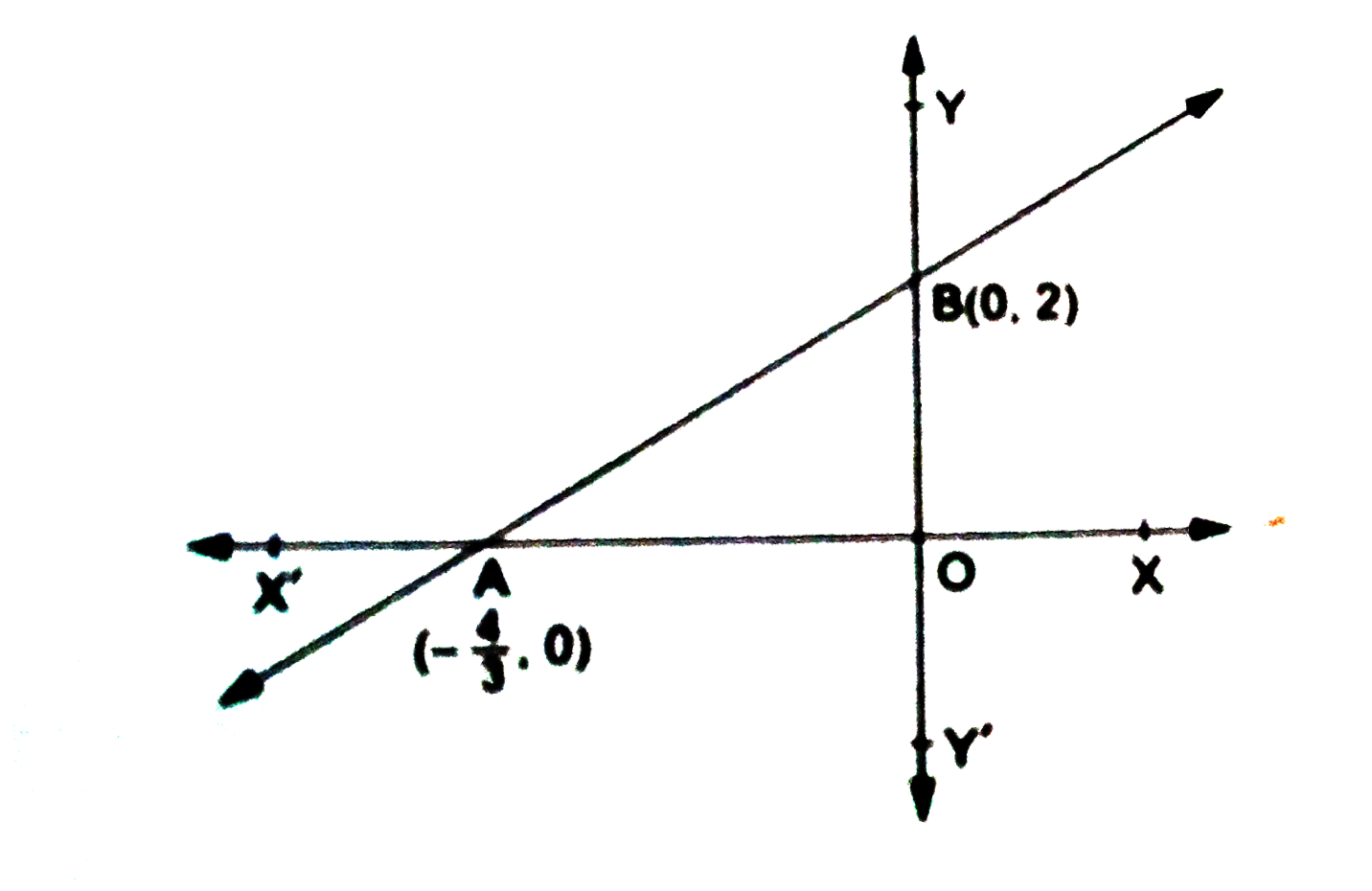
∴x(−43)+y2=1 is the required equation in intercepts form.
x-intercept =−43 and y-intercept =2
If AB is the part of the line intercepted between the axes them the end points of this line segment are A(−43,0)andB(0,2)
Length of AB=√(−43,−0)2+(0−2)2=√169+4=23sqrt13units
Topper's Solved these Questions
- BOOK - RS AGGARWALCHAPTER - STRAIGHT LINES EXERCISE - EXAMPLE56videos
STRAIGHT LINES
- BOOK - RS AGGARWALCHAPTER - STRAIGHT LINES EXERCISE - SOLVED-EXAMPLE12videos
STRAIGHT LINES
- BOOK - RS AGGARWALCHAPTER - STATISTICSEXERCISE - EXERCISE 30D5videos
STATISTICS
- BOOK - RS AGGARWALCHAPTER - THREE-DIMENSIONAL GEOMETRY EXERCISE - EXERCISE 26 C13videos
THREE-DIMENSIONAL GEOMETRY
Similar Questions
Reduce the equation x+2y=3 to the intercept form.
View SolutionReduce the equation 3x−2y+6=0 to the intercept form and find the x and y intercepts.
View SolutionReduce the equation 3x-4y+12=0 to intercepts form. Hence, find the length of the portion of the line intercepted between the axes.
View SolutionReduce the equation 5x-12y=60 to intercepts form. Hence, find the length of the portion of the line intercepted between the axes.
View SolutionReduce the equation 2x-3y-5=0 to slope-intercept form, and find from it the slope and y-intercept
View SolutionReduce the equations to the intercept form 3x−4y=10
View SolutionReduce the equations to the intercept form 4x−3y=6
View SolutionReduce the equations to the intercept form 2x−3y=5
View SolutionReduce the equation y+5=0 to slope-intercept form, and hence find the slope and the y-intercept of the line.
View SolutionReduce the equation 6x+3y−5=0 to the slope-intercept form and find its slope and y-intercept.
View Solution

