S and T are points on sides PR and QR of such that Show that
To prove that triangles ΔRPQ and ΔRTS are similar, we will use the Angle-Angle (AA) similarity criterion.
1. Given Information:
- We have triangle PQR.
- Points S and T are located on sides PR and QR respectively.
- It is given that ∠P=∠RTS.
2. Identify Angles:
- Let ∠P=∠RTS (this is given).
- Let ∠QRP be ∠3 (common angle).
- We need to show that ∠RST is equal to ∠RPQ.
3. Common Angle:
- Notice that ∠QRP is common to both triangles ΔRPQ and ΔRTS.
- Thus, we can state that ∠QRP=∠QRP.
4. Applying AA Criterion:
- We have two pairs of angles:
- ∠P=∠RTS
- ∠QRP=∠QRP (common angle).
- Therefore, by the AA similarity criterion, since two angles of triangle RPQ are equal to two angles of triangle RTS, we can conclude that:
ΔRPQ∼ΔRTS
5. Conclusion:
- Hence, we have shown that ΔRPQ is similar to ΔRTS.
- We have triangle PQR.
- Points S and T are located on sides PR and QR respectively.
- It is given that ∠P=∠RTS.
- Let ∠P=∠RTS (this is given).
- Let ∠QRP be ∠3 (common angle).
- We need to show that ∠RST is equal to ∠RPQ.
- Notice that ∠QRP is common to both triangles ΔRPQ and ΔRTS.
- Thus, we can state that ∠QRP=∠QRP.
- We have two pairs of angles:
- ∠P=∠RTS
- ∠QRP=∠QRP (common angle).
- Therefore, by the AA similarity criterion, since two angles of triangle RPQ are equal to two angles of triangle RTS, we can conclude that:
ΔRPQ∼ΔRTS
- Hence, we have shown that ΔRPQ is similar to ΔRTS.
Topper's Solved these Questions
- BOOK - NAGEEN PRAKASHAN ENGLISHCHAPTER - TRIANGLES EXERCISE - Problems From NCERT/ Exemplar14videos
TRIANGLES
- BOOK - NAGEEN PRAKASHAN ENGLISHCHAPTER - TRIANGLES EXERCISE - Exercise 6a24videos
TRIANGLES
- BOOK - NAGEEN PRAKASHAN ENGLISHCHAPTER - STATISTICS EXERCISE - Revision Exercise Long Answer Questions4videos
STATISTICS
- BOOK - NAGEEN PRAKASHAN ENGLISHCHAPTER - VOLUME AND SURFACE AREA OF SOLIDSEXERCISE - Revisions Exercise Long Answer Questions5videos
VOLUME AND SURFACE AREA OF SOLIDS
Similar Questions
S and T are points on sides PR and QR of ΔPQR such that ∠P=∠RTS. Show that ΔRPQ~ΔRTS.
View SolutionIn figure ,D and E are Points on side BC of a ΔABC such that BD=CE and AD=AE. Show that ΔABD≅ΔACE.
 View Solution
View SolutionS is any point on side QR of a ΔPQR. Show that PQ+QR+RP>2PS .
View SolutionS and T are points on the sides PQ and PR, respectively of ΔPQR, such that PT = 2 cm, TR = 4 cm and ST is parallel to QR. Find the ratio of the areas of ΔPST and ΔPQR.
View SolutionIn a triangle PQR, L and M are two points on the base QR, such that ∠LPQ=∠QRP and ∠RPM=∠RQP. Prove that:
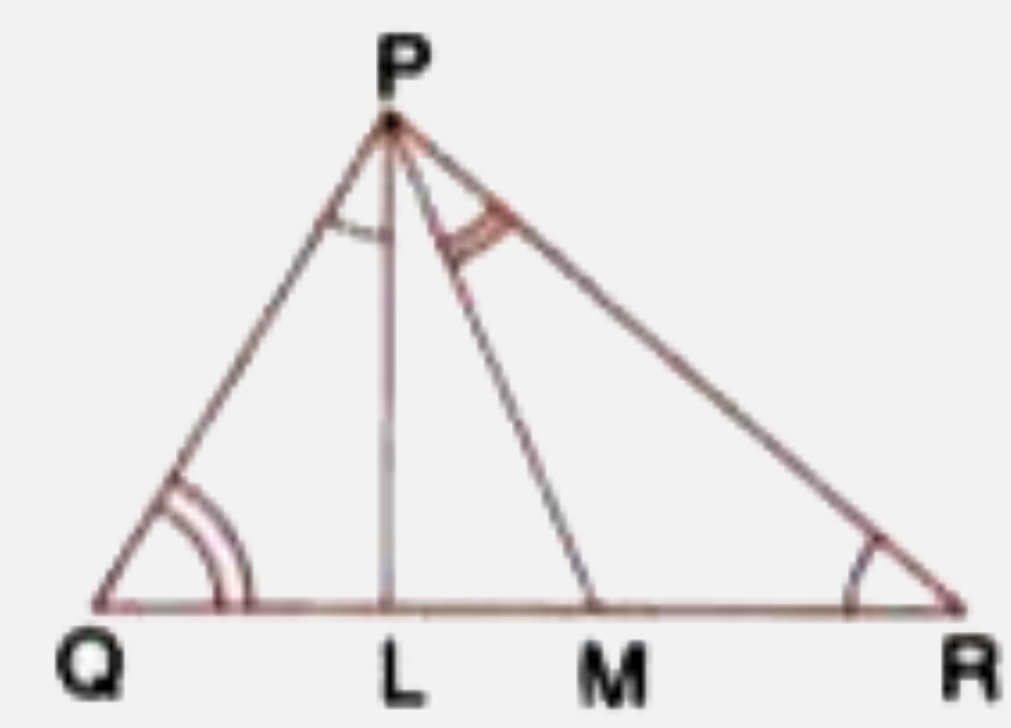
ΔPQL~ΔRPMView SolutionIf Q is a point on the side SR of a triangle ΔPSR such that PQ=PR then prove that PS>PQ
View SolutionA and B are respectively the points on the sides PQ and PR of a ΔPQR such that PQ =12.5 cm, PA= 5 cm, BR = 6 cm and PB = 4 cm. Is AB || QR? Give reason for your answer.
View SolutionPQR is a triangle. S is a point on the side QR of ΔPQR such that ∠PSR=∠QPR. Given QP = 8 cm, PR = 6 cm and SR = 3 cm.

area of ΔPQRarea of ΔSPRView SolutionPQR is a triangle. S is a point on the side QR of ΔPQR such that ∠PSR=∠QPR. Given QP = 8 cm, PR = 6 cm and SR = 3 cm.

Find the lengths of QR and PS.View SolutionPQR is a triangle. S is a point on the side QR of ΔPQR such that ∠PSR=∠QPR. Given QP = 8 cm, PR = 6 cm and SR = 3 cm.

Prove ΔPQR~ΔSPR.View Solution

