Show that sin(cot−1(tancos−1x))=xSolution in Bengali
For θ=cos−1x, we have the following triangle

∴E=sin(cot−1(tan(cos−1x)))
=sin(cot−1(tan(tan−1.√1−x2x)))
=sin(cot−1.√1−x2x)
Now, for α=cot−1(√1−x2)x, we have following triangle
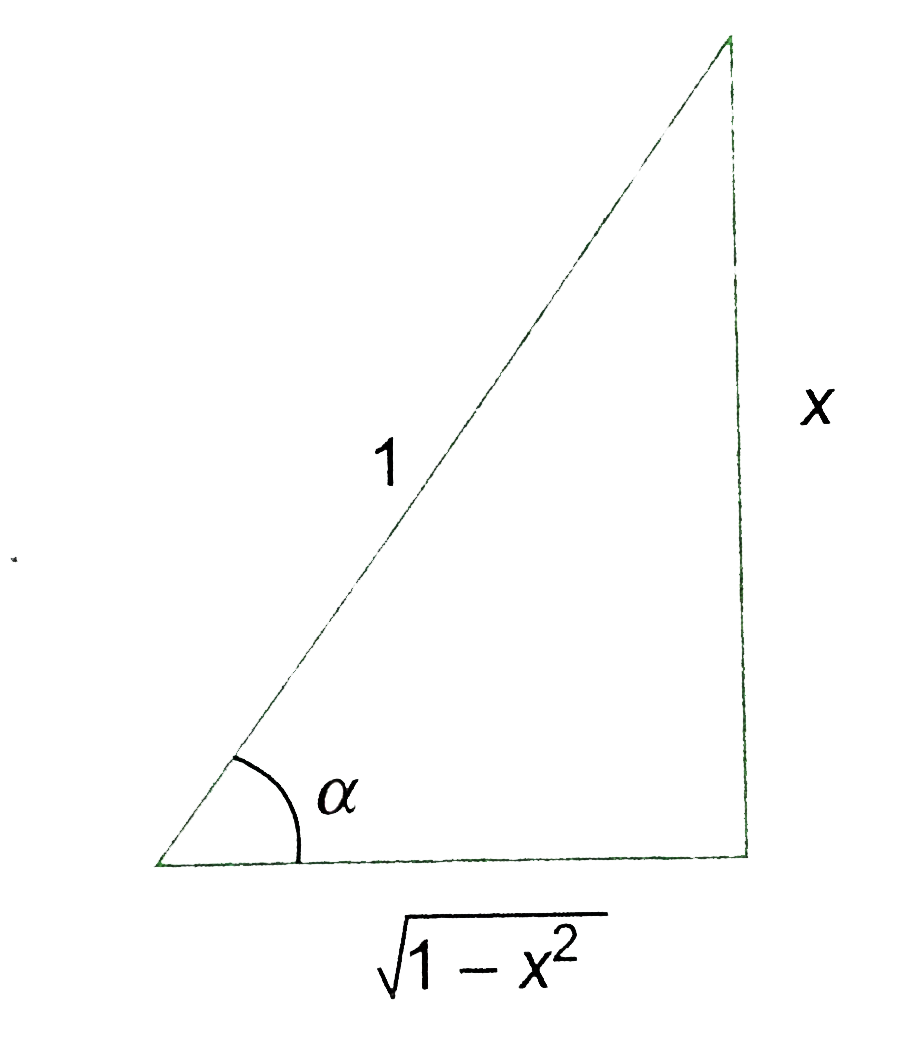
∴E=sin(sin−1.x1)=x
Topper's Solved these Questions
Similar Questions
The points with position vectors →x+→y,→x−→yand→x+λ→y are collinear for all real values of λ.
View SolutionIf y = y(x) is the solution of the differential equation, xdydx+2y=x2 satisfying y(1) = 1, then y(12) is equal to
View SolutionIf A=sin[cot^(-1){cos(tan^(-1)x)}], then
View SolutionProve that sincot−1tancos−1x=sincosec−1cottan−1x=x, where x∈[0,1]
View SolutionIf sin[cot^(-1)(1+x)]=cos(tan^(-1)x) Then x =
View SolutionIf sin{cot^(-1)(1+x)}=cos(tan^(-1)x) Then x =
View Solutionsin{cot^(-1)[cos(tan^(-1)x)]}=....
View Solutionsin{cot−1[tan(cos−1x)]=
View Solutionsin(Cot^(-1)(cos(Tan^(-1)x)))=
View SolutionIf sin (cot^(-1)(1-x))=cos(tan^(-1)(-x)) , then x is
View Solutioncos[tan−1{sin(cot−1x)}]=
View Solutioncos[tan−1{sin(cot−1x)}]=
View SolutionProve that sincot−1tancos−1x=sincosec−1cottan−1x=x, where x∈[0,1]
View SolutionIf x=cosec[tan−1{cos(cot−1(sec(sin−1a)))}] and y=sec[cot−1{sin(tan−1(cosec(cos−1a)))}] show that x = y
View Solutionsin[cot^(-1){cos(tan^(-1)x)}]=
View SolutionShow that cosA1−tanA+sinA1−cotA=sinA+cosA
View Solution
