Show that the diagonals of a square are equal and bisect each other at right angles.
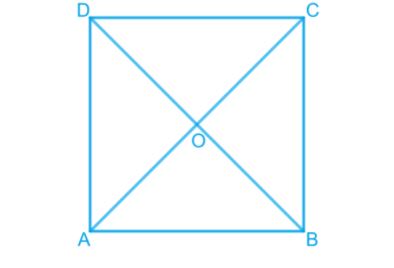
Given: The quadrilateral is a square.
To prove: Diagonals of a square are equal and bisect each other at right angles.
Thus, we have to prove, and
Letbe a square.
Let the diagonals and intersect each other at a point .
In and ,
(Sides of a square are equal to each other)
(All interior angles are of 90^@)
(Common side)
(By SAS congruence rule)
(By CPCT) ------------ (1)
Hence, the diagonals of a square are equal in length.
In and ,
(Vertically opposite angles)
(Alternate interior angles)
(Sides of a square are always equal)
(By AAS congruence rule)
and (By CPCT) ------------ (2)
Hence, the diagonals of a square bisect each other.
In and ,
As we had proved that diagonals bisect each other,
Therefore,
(Sides of a square are equal)
(Common)
(By SSS congruency)
(By CPCT) --------- (3)
However, (Linear pair)
[From equation (3)]
------------- (4)
Hence, from equation (1), (2) and (4), we see that the diagonals of a square are equal and bisect each other at right angles
Topper's Solved these Questions
- BOOK - NCERT ENGLISHCHAPTER - QUADRILATERALSEXERCISE - SOLVED EXAMPLES8videos
QUADRILATERALS
- BOOK - NCERT ENGLISHCHAPTER - QUADRILATERALSEXERCISE - Exercise 8.27videos
QUADRILATERALS
- BOOK - NCERT ENGLISHCHAPTER - PROBABILITYEXERCISE - SOLVED EXAMPLES10videos
PROBABILITY
- BOOK - NCERT ENGLISHCHAPTER - STATISTICSEXERCISE - Exercise 14.29videos
STATISTICS
Similar Questions
Show that if the diagonals of a quadrilateral are equal and bisect each other at right angle, then it is a square.
View SolutionShow that if the diagonals of a quadrilateral are equal and bisect each other at right angles, then it is a square
View SolutionShow that if the diagonals of a quadrilateral bisect each other at right angles, then it is a rhombus.
View SolutionShow that if the diagonals of a quadrilateral bisect each other at right angles, then it is a rhombus.
View SolutionProve that; If the diagonals of a quadrilateral bisect each other at right angles, then it is a rhombus.
View SolutionProve that the diagonals of a parallelogram bisect each other.
View SolutionShow that the diagonals of a rhombus are perpendicular to each other
View SolutionShow that the diagonals of a rhombus are perpendicular to each other
View SolutionState True or False
If the diagonals of a quadrilateral bisect each other at right angle, the quadrilateral is a square.View SolutionFill in the blanks, in each of the following, so as to make the statement true: 1. A rhombus is a parallelogram in which.... 2. A square is a rhombus in which.... 3. A rhombus has all its sides of ........ length. 4. The diagonals of a rhombus..... each other at... angles. 5.It the diagonals of a parallelogram bisect each other at right angles, then it is a....
View Solution

