Show that the quadrialteral formed by joining the mid-points of the consecutive sides of a rhombus, is a rectangle.
To show that the quadrilateral formed by joining the midpoints of the consecutive sides of a rhombus is a rectangle, we can follow these steps:
Step 1: Define the Rhombus
Let the vertices of the rhombus be A,B,C,D. By definition, a rhombus has all sides equal, i.e., AB=BC=CD=DA.
Step 2: Identify Midpoints
Let P,Q,R,S be the midpoints of sides AB,BC,CD, and DA respectively.
Step 3: Use the Midpoint Theorem
According to the Midpoint Theorem, the line segment joining the midpoints of two sides of a triangle is parallel to the third side and half its length.
Step 4: Analyze Triangle ABC
In triangle ABC:
- P is the midpoint of AB and Q is the midpoint of BC.
- Therefore, segment PQ is parallel to AC and PQ=12AC.
Step 5: Analyze Triangle ADC
In triangle ADC:
- S is the midpoint of DA and R is the midpoint of CD.
- Thus, segment SR is parallel to AC and SR=12AC.
Step 6: Establish Parallelism
From the above steps, we have:
- PQ∥SR and PQ=SR.
Step 7: Analyze Triangles ABP and CDQ
- Since P and Q are midpoints, AP=PB and CQ=QD.
- Therefore, PS∥QR and PS=QR (by the same reasoning).
Step 8: Establish Rectangle Properties
Since PQ∥SR and PS∥QR, quadrilateral PQRS is a parallelogram.
Additionally, since P and Q are midpoints, the angles ∠PQR and ∠PSR are right angles (because diagonals of a rhombus bisect each other at right angles).
Step 9: Conclusion
Since PQRS is a parallelogram with one angle being 90∘, it follows that PQRS is a rectangle.
Final Statement
Thus, we have shown that the quadrilateral formed by joining the midpoints of the consecutive sides of a rhombus is a rectangle.
---
Let the vertices of the rhombus be A,B,C,D. By definition, a rhombus has all sides equal, i.e., AB=BC=CD=DA.
Let P,Q,R,S be the midpoints of sides AB,BC,CD, and DA respectively.
According to the Midpoint Theorem, the line segment joining the midpoints of two sides of a triangle is parallel to the third side and half its length.
In triangle ABC:
- P is the midpoint of AB and Q is the midpoint of BC.
- Therefore, segment PQ is parallel to AC and PQ=12AC.
In triangle ADC:
- S is the midpoint of DA and R is the midpoint of CD.
- Thus, segment SR is parallel to AC and SR=12AC.
From the above steps, we have:
- PQ∥SR and PQ=SR.
- Since P and Q are midpoints, AP=PB and CQ=QD.
- Therefore, PS∥QR and PS=QR (by the same reasoning).
Since PQ∥SR and PS∥QR, quadrilateral PQRS is a parallelogram.
Additionally, since P and Q are midpoints, the angles ∠PQR and ∠PSR are right angles (because diagonals of a rhombus bisect each other at right angles).
Since PQRS is a parallelogram with one angle being 90∘, it follows that PQRS is a rectangle.
Thus, we have shown that the quadrilateral formed by joining the midpoints of the consecutive sides of a rhombus is a rectangle.
Topper's Solved these Questions
- QUADRILATERALSBOOK - NAGEEN PRAKASHAN ENGLISHCHAPTER - QUADRILATERALSEXERCISE - Revision Exercise (very Short Answer Questions)
10 Videos
- QUADRILATERALSBOOK - NAGEEN PRAKASHAN ENGLISHCHAPTER - QUADRILATERALSEXERCISE - Revision Exercise (short Answer Questions )
10 Videos
- QUADRILATERALSBOOK - NAGEEN PRAKASHAN ENGLISHCHAPTER - QUADRILATERALSEXERCISE - Exercise 8a
29 Videos
- PROBABILITYBOOK - NAGEEN PRAKASHAN ENGLISHCHAPTER - PROBABILITYEXERCISE - Revision Exercise (very Short Answer /short Answer Questions)
10 Videos
- STATISTICSBOOK - NAGEEN PRAKASHAN ENGLISHCHAPTER - STATISTICSEXERCISE - Revision Exercise
12 Videos
Similar Questions
Show that the quadrilateral formed by joining the mid-points of the consecutive sides of a rectangle is a rhombus.
View SolutionShow that the quadrilateral formed by joining the mid-points of the consecutive sides of a rectangle is a rhombus.
View SolutionShow that the quadrilateral formed by joining the mid-points of the consecutive sides of a rectangle is a rhombus.
View SolutionThe diagonals of a quadrilateral ABCD are mutually perpendicular . Prove that the quadrilateral formed by joining the mid-points of its consecutive sides is a reactangle.
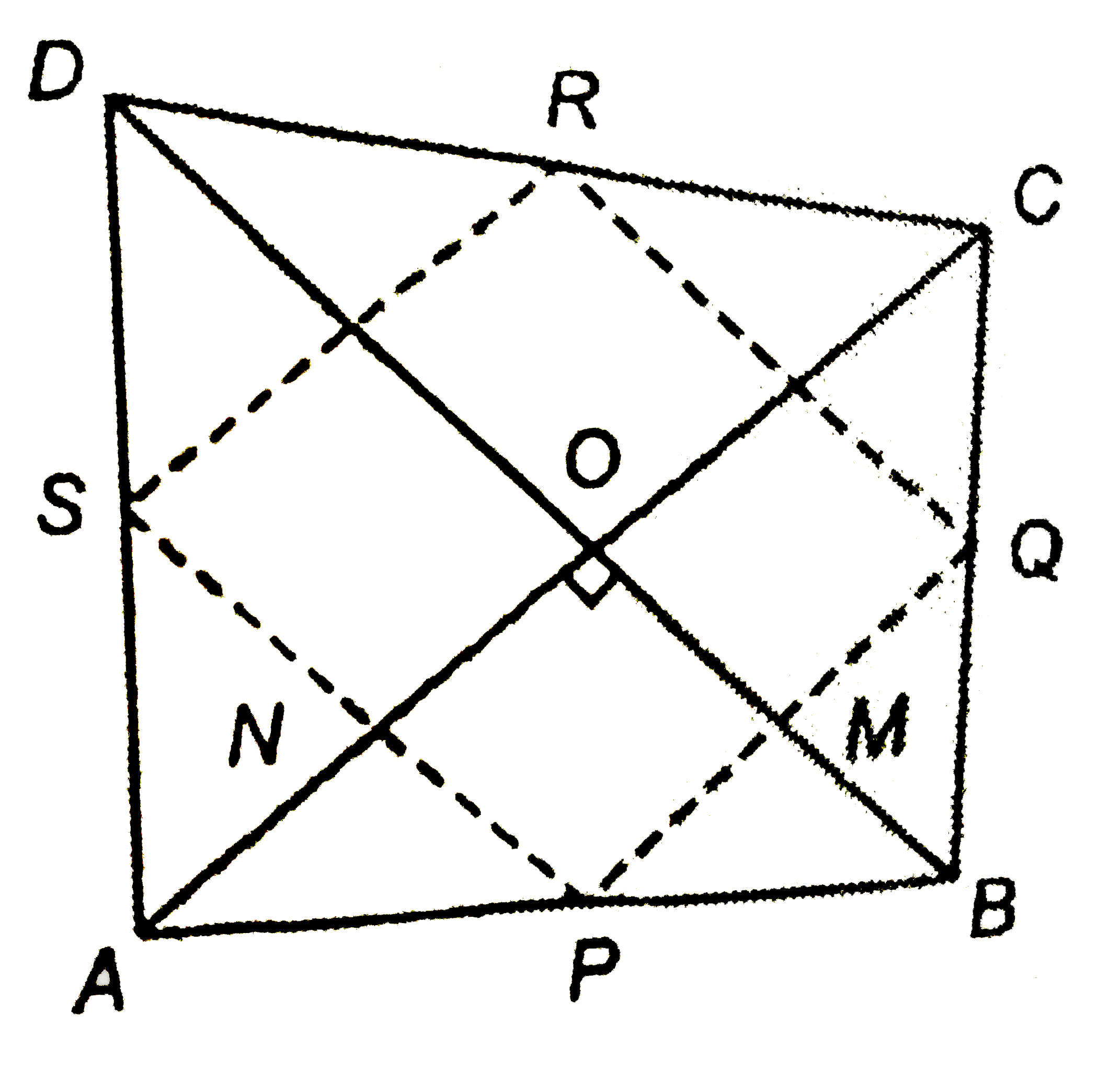
View SolutionThe diagonals of a quadrilateral ABCD are perpendicular. Show that the quadrilateral, formed by joining the mid-points of its sides, is a rectangle.
View SolutionThe diagonals of a quadrilateral ABCD are perpendicular. Show that the quadrilateral, formed by joining the mid-points of its sides, is a rectangle.
View SolutionShow that the quadrilateral, formed by joining the mid-points of the sides of a square, is also a square.
View SolutionShow that the quadrilateral, formed by joining the mid-points of the sides of a square is also a square.
View SolutionShow that the quadrilateral, formed by joining the mid-points of the sides of a square is also a square.
View SolutionProve that the quadrilateral formed by joining the mid-points of the pairs of consecutive sides of a quadrilateral is a parallelogram.
View Solution
