Sides AB and BC and median AD of a triangle ABC are respectively proportional to sides PQ and QR and median PM of . Show that .
We have,
In , We have
[ from(i)]
[ by SSS- similarity]
And so, . [ crosses. angles of similar triangels are equal]
Now, in , we have
[ proved above]
[from (i)]
[ by SAS- similarity]
Topper's Solved these Questions
- TRIANGLESBOOK - RS AGGARWALCHAPTER - TRIANGLESEXERCISE - SOLVED EXAMPLE
4 Videos
- TRIANGLESBOOK - RS AGGARWALCHAPTER - TRIANGLESEXERCISE - EXERCISE 7 A
1 Videos
- T-RATIOS OF SOME PARTICULAR ANGLESBOOK - RS AGGARWALCHAPTER - T-RATIOS OF SOME PARTICULAR ANGLESEXERCISE - Exercise 11
27 Videos
- TRIGONOMETRIC IDENTITIESBOOK - RS AGGARWALCHAPTER - TRIGONOMETRIC IDENTITIESEXERCISE - Test Yourself
20 Videos
Similar Questions
Sides AB and AC and median AD of a triangle ABC are respectively proportional to sides PQ and PR and median PM of another triangle PQR. Show that ΔABC~ΔPQR.
View SolutionSides AB and BC and median AD of a triangle ABC are respectively propor-/ tional to sides PQ and QR and median PM of ΔPQR (see Fig. 6.41). Show that ΔABC~ΔPOR.
View Solution
Knowledge Check
In the given figure, the two sides AB and BC, and the median AD of ΔABC are correspondingly equal to the two sides PQ and QR, and the medium PM of ΔPQR. Prove that ΔABC≅ΔPQR.
AΔABD≅ΔPQMBΔABC≅ΔPQRCΔABD≅ΔPMRDΔADC≅ΔPMR
Sides AB and AC and median AD of a triangle ABC are respectively proportional to sides PQ and PR and median PM of another triangle PQR. Prove that ΔABC~DetlaPQR
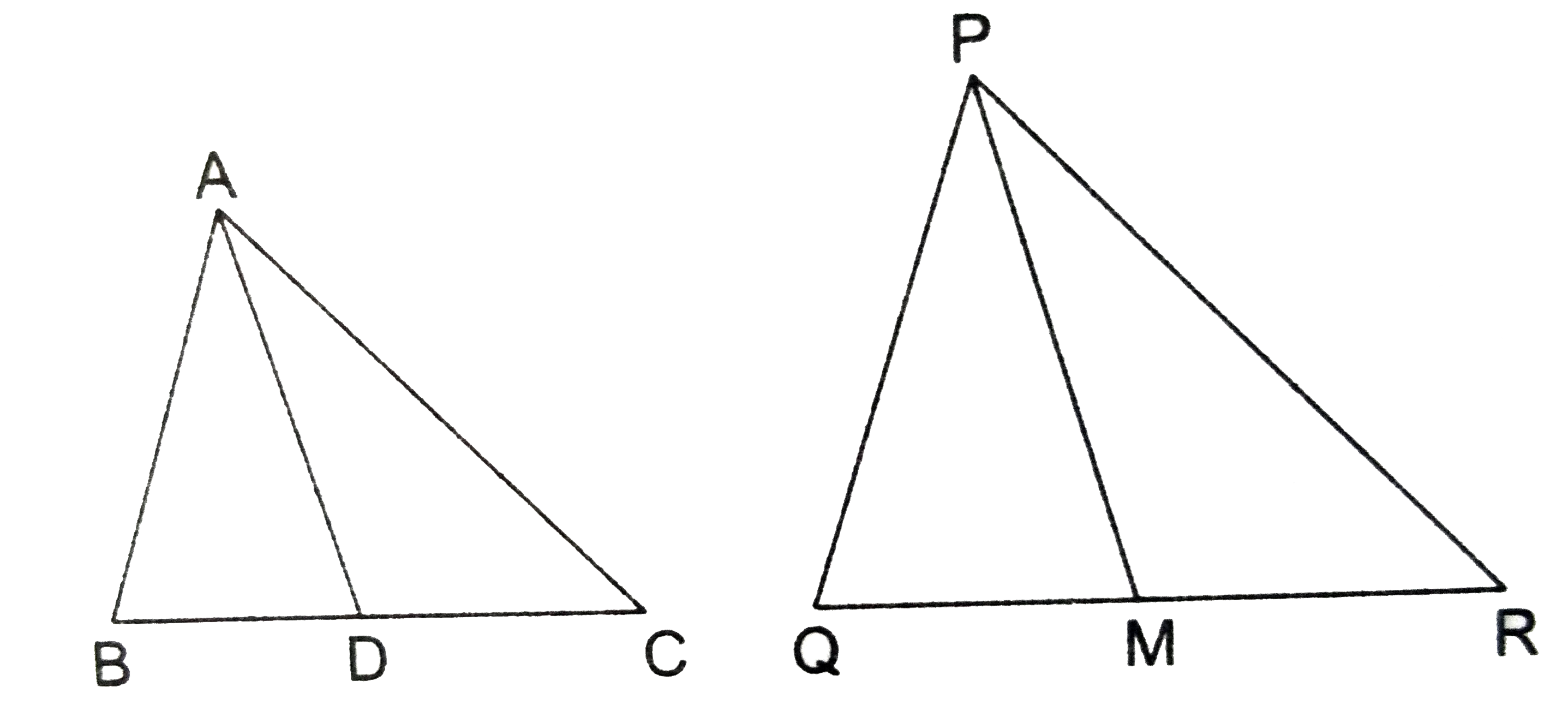
View SolutionThe sides AB and BC and the median AD of triangle ABC are equal to the sides PQ and QR and the median PM of triangle PQR respectively. Prove that the triangles ABC and PQR are congruent.
View SolutionTwo sides AB and BC and median AM of one triangle ABC are respectively equal to sides PQ and QR and median PN of ΔPQR (see figure). Show that

ΔABM≅ΔPQN
View SolutionTwo sides AB and BC and median AM of one triangle ABC are respectively equal to side PQ and QR and median PN of ΔABC≅ΔPQR(see Fig. 7.40). Show that:
(i) ΔABM≅ΔPQN
(ii) ΔABC≅ΔPQR
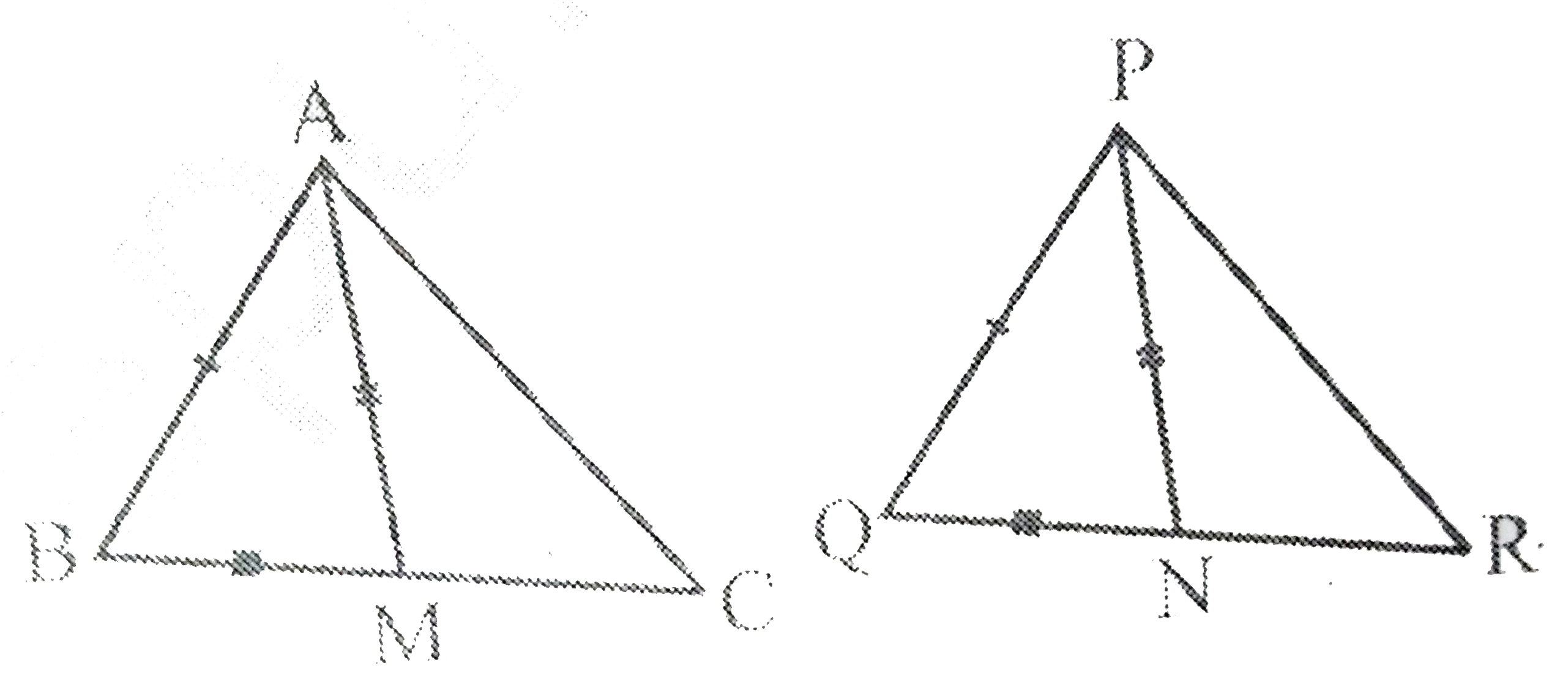
View SolutionIn the given figure, the two sides AB and BC, and the median AD of ΔABC are correspondingly equal to the two sides PQ and QR, and the medium PM of ΔPQR. Prove that ΔABC≅ΔPQR.
View SolutionThe sides AB and BC and the median AD of triangle ABC are equal to the sides PQ and QR and the median PM of triangle PQR respectively. Prove that the triangles ABC and PQR are congruent.
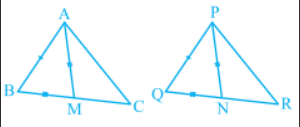
View SolutionIn Figure, two sides AB and BC and the median AD of ABC are equal respectively to the two sides PQ and QR and the median PM of the other triangle PQR. Prove that ABD≅PQM (ii) ABC ≅ PQR
View Solution
