sin(tan−1x),|x|≤1 is equal to :
A
x√1−x2
B
1√1−x2
C
1√1+x2
D
x√1+x2
Video Solution
Text Solution
The correct Answer is:D
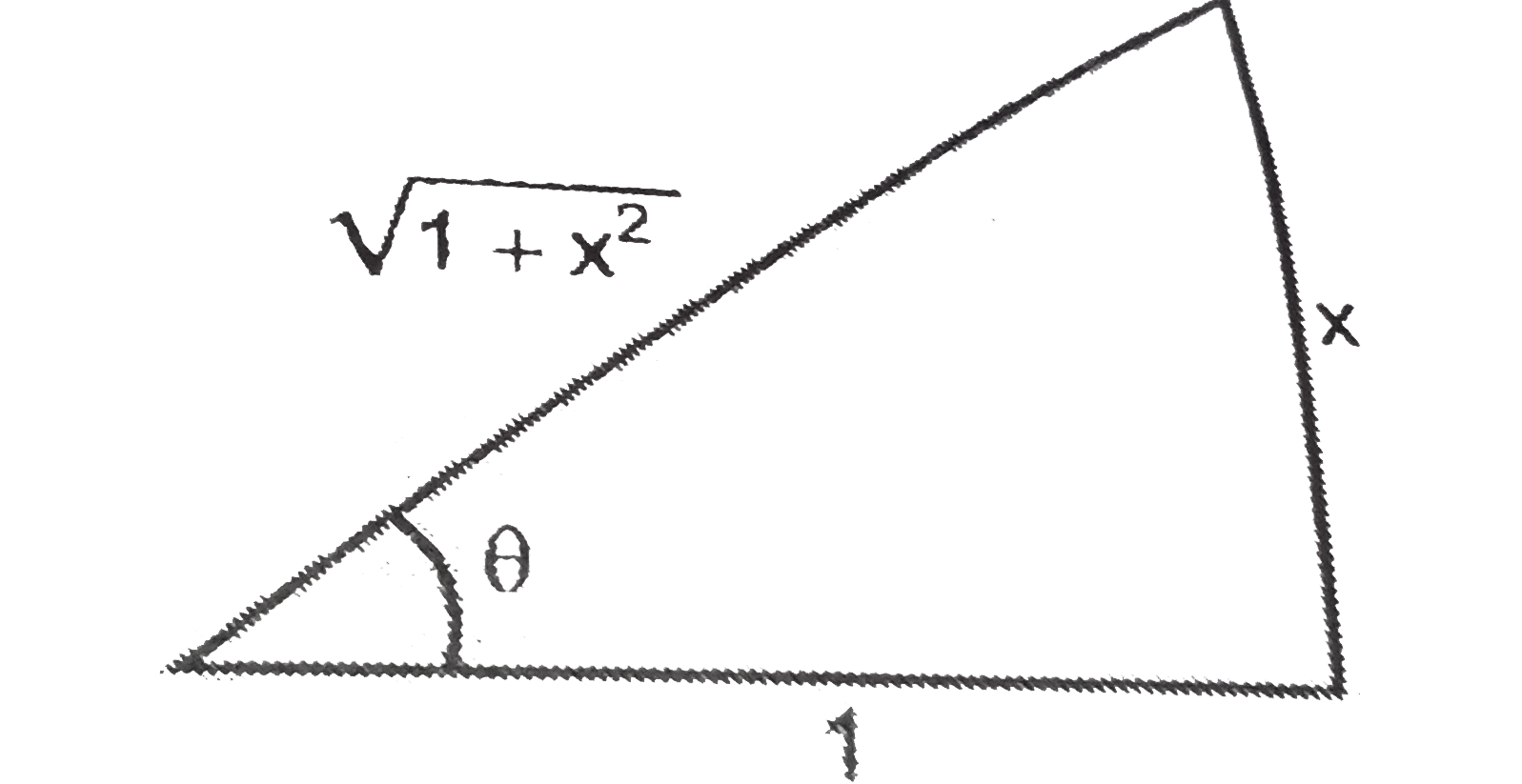
sin(tan−1x)=sinθ Let tan−1x=θ
=x√1+x2 ⇒xtanθ
|
Topper's Solved these Questions
- INVERES TRIGONOMETRIC FUNCTIONSBOOK - NAGEEN PRAKASHANCHAPTER - INVERES TRIGONOMETRIC FUNCTIONSEXERCISE - Miscellaneous Exercise
8 Videos
- INTEGRATIONBOOK - NAGEEN PRAKASHANCHAPTER - INTEGRATIONEXERCISE - Miscellaneous Exercise
44 Videos
- LINEAR PROGRAMMINGBOOK - NAGEEN PRAKASHANCHAPTER - LINEAR PROGRAMMINGEXERCISE - Miscellaneous Exercise
9 Videos
Similar Questions
Knowledge Check
sin(tan−1x),wheren |x|<1 is equal to :
Ax√1−x2B1√1−x2C1√1+x2Dx√1+x2The value of sin(2tan−1x),|x|≤1 is
A1/xBxC1/x2D2x/(1+x2)∫tan(sin−1x)dx is equal to
A1√1−x2+CB√1−x2+CC−x√1−x2+CDx√1−x2+C
Number of solutions of tan(sin−1x)+sin(tan−1x)=x is equal to
View Solutionsin(tan−1x), where |x|<1, is equal to:
View SolutionIf f(x)=√1+sin−1x1−tan−1x, then f (0) is equal to :
View SolutionIf f(x)=√1+sin−1x1−tan−1x, then f'(0) is equal to:
View SolutionThe value of lim|x|→∞cos(tan−1(sin(tan−1x))) is equal to
View Solution
